Use the Partial Differential Equations VIs to solve partial differential equations (PDE), including the Helmholtz, heat, and wave equations. The following table provides details about these equations.

Note The Partial Differential Equations VIs are available only in the LabVIEW Full and Professional Development Systems.
Type of Equation Dimension and Domain Boundary Condition Method
Helmholtz equation The equation is two-dimensional and defined in a rectangular or polygonal domain. The polygonal domain supports only the Dirichlet condition. The rectangular domain supports the Dirichlet and Neumann conditions. The finite element method solves the equation defined on the polygonal domain. The finite difference method solves the equation defined on the rectangular domain.
Heat equation The equation is one-dimensional or two-dimensional and defined on the rectangular domain. The equation supports the Dirichlet and Neumann conditions. The finite difference method solves this equation.
Wave equation The equation is one-dimensional or two-dimensional and defined on the rectangular domain. The equation supports the Dirichlet and Neumann conditions. The finite difference method solves this equation.

The following block diagram examples show a common order for solving PDEs with the VIs. While you can add the VIs to the block diagram in the order they appear in the two examples, you do not need to follow that order when you use the PDE VIs. The following list provides an example of an order you can use when you want to solve PDEs with the VIs.

  • Define PDE
  • Define PDE Domain
  • Define PDE Boundary Condition
  • Define PDE Initial Condition
  • PDE Solver
  • PDE Rendering

The following block diagram illustrates an example of how to solve a 1D wave equation.

Note The polymorphic instance you choose must match the type of equation you need to solve. The type of instance also needs to be consistent from step to step. Otherwise, LabVIEW returns a type conflict error.

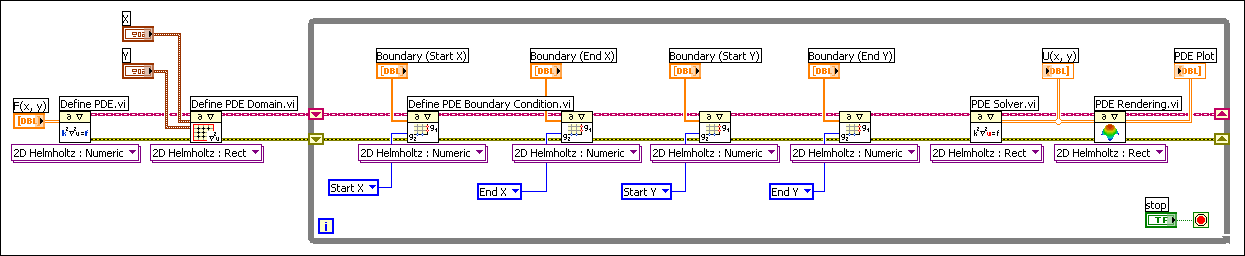
The following block diagram illustrates an example of how to solve a Helmholtz equation in a loop. The coefficient, the right side of the equation, and the domain of the equation do not change during the execution. While you do not need to repeatedly define the equation and domain in the loop, the boundary values vary over time. Therefore, you only need to place the definition of the boundary condition in the loop. In the following block diagram example, a shift register of a While Loop implements the PDE class to transfer data from one iteration to the next.

Related information Partial Differential Equations VIs Define PDE VI Define PDE Domain VI Define PDE Boundary Condition VI Define PDE Initial Condition VI PDE Solver VI PDE Rendering VI