1D数値積分
- 更新日2025-07-30
- 5分で読める
4つの一般的な数値積分法のうちの1つを使用して、データの入力配列の数値積分を実行します。
入力配列入力にデータを配線して自動的に多態性インスタンスを決定するか、インスタンスを手動で選択 します。
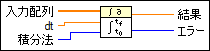
入力/出力
 入力配列
—
入力配列
—
入力配列には、dtの倍数、すなわちf(0)、f(dt)、f(2dt)、…で被積分関数f(t)をサンプルすることで得られる積分されるデータが含まれます。  dt
—
dt
—
dtは間隔のサイズで、関数から入力配列のデータを得るのに使用するサンプリングステップサイズを表します。 負のdtを使用する場合、このVIはその絶対値を使用します。  積分法
—
積分法
—
積分法は、数値積分を実行するのに使用する方法を指定します。
 結果
—
結果
—
結果は数値積分を返します。  エラー
—
エラー
—
エラーは、VIからのエラーまたは警告を返します。エラーは「エラーコードからエラークラスタ」VIに配線して、エラーコードまたは警告をエラークラスタに変換できます。 |
このVIに配線するx値は等間隔である必要があり、そうでない場合、結果は不正確になります。値が等間隔でない場合は、「非一様数値積分」VIを使用して積分を計算できます。
1D数値積分
| ポイント数 | 実行される部分評価 |
|---|---|
| 224 | 55 Bode, 1 Simpsons' 3/8 |
| 225 | 56 Bode |
| 226 | 56 Bode, Trapezoidal |
| 227 | 56 Bode, 1 Simpsons' |
| 228 | 57 Bode, 1 Simpsons' 3/8 |
224ポイントが用意されており、Bode方式が選択されている場合、VIは、55 Bode方式部分評価と1回のSimpsonsの3/8方式評価を実行することで結果を求めます。
各方式は、サンプリング間隔 (dt) に依存し、ある特定の数の隣接するポイントによって異なる部分評価を実行するために、基本公式の連続的な適用を行うことで積分を求めます。各部分評価に使用されるポイント数は、その方式の次数を表します。結果は、これらの連続的な部分評価の和です。
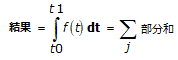
ここで、jはポイント数と積分法に依存する範囲です。
以下は、昇順の各方式の部分和を計算する基本公式です。
- Trapezoidal: 1/2(x[i] + x[i + 1])*dt
- Simpsons': (x[2i] + 4x[2i + 1] + x[2i + 2])*dt/3, k = 2
- Simpsons' 3/8: (3x[3i] + 9x[3i + 1] + 9x[3i + 2] + 3x[3i + 3]) * dt/8, k = 3
-
ボーデ(14x[4i] +64x[4i + 1] +24x[4i + 2] +64x[4i + 3] +14x[4i + 4]) * dt/45、 k = 4
for i = 0, 1, 2, 3, 4, ..., [(N - 1)/k] の積分部分。
ここで、Nはデータポイントの数、kは各方式に依存する整数、xは入力配列です。