Periodicity, Leakage, and Windowing

Periodicity is a basic assumption made in FFT-based frequency analysis. The FFT algorithm implicitly assumes that every block of acquired data indefinitely repeats in both positive and negative time. When the input signal is not periodic within the block, energy appears to leak into neighboring spectral bins. This spectral leakage can hide and/or distort low-amplitude spectral components. Windowing both ensures periodicity and limits leakage.

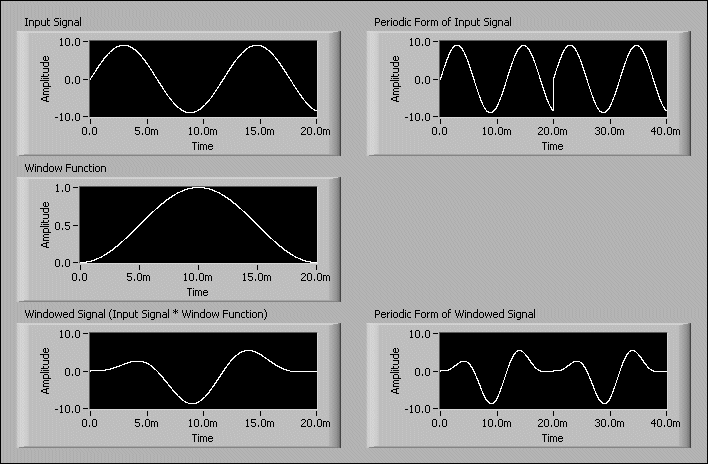
Windowing multiplies the time-domain data by a window function before the FFT is performed. Window functions typically have a value of zero at the start and end of the measurement period. The following figure shows how a signal that is not the same at the start and end of the measurement period appears not to be periodic and how the signal becomes periodic when multiplied by a window function.

Figure 35. Signal Windowing

1378

The windows that the NI Sound and Vibration Measurement Suite supports and their equivalent noise bandwidths (ENBW) are listed in the following table.

Table 5. Supported Windows and Their Equivalent Noise Bandwidths
Window Equivalent Noise Bandwidth (ENBW)
None 1
Hanning 1.50
Hamming 1.36
Blackman-Harris 1.71
Exact Blackman 1.69
Blackman 1.73
Flat Top 3.77
4 Term Blackman-Harris 2.00
7 Term Blackman-Harris 2.63
Low Sidelobe 2.22
Blackman Nuttall 1.98
Triangle 1.33
Barlett-Hanning 1.46
Bohman 1.79
Parzen 1.92
Welch 1.20
Kaiser 3.85
Dolph-Chebyshev 1.40
Gaussian 1
Force-Exponential N/A

ENBW is a property of the window applied to the signal. Typically, you use a window with a low ENBW to resolve peak frequencies. You use a window with a high ENBW to resolve peak amplitudes. Use the Force-Exponential window for shock and impulse testing where the stimulus signal exhibits transient behavior after the impact event, or where the response of the signal does not decay to zero in the measurement period.