ピボット列を使用して、または使用しないでAのQR分解を行います。A入力にデータを配線して自動的に使用する多態性インスタンスを決定するか、インスタンスを手動で選択します。


icon

入力/出力

  • c2dcdb.png A —

    Aはm × nの複素行列です。ここで、mはAの行数、nはAの列数です。Aには正方行列または矩形行列を指定できます。

  • cbool.png ピボット? —

    ピボット?は、このVIでピボット列を使用してAを分解するかどうかを指定します。ピボット?がTRUEの場合、このVIは、AP=QRの式に従ってAを分解します。このVIは、降順でRの対角数の絶対値を返します。ピボット?がFALSEの場合、このVIは、A=QRの式に従ってAを分解します。デフォルトはFALSEです。

  • cu16.png Qオプション —

    Qオプションは、このVIでQを生成する方法を指定します。

    Qオプションは以下の値のうち1つを使用する必要があります。ここで、m はAの行数、n はAの列数です。

    0フルサイズQ (デフォルト)―Qのサイズはm x mで、Rのサイズはm x nです。
    1エコノミーサイズQ―Qのサイズはm x min(m, n)で、Rのサイズはmin(m, n) x nです。
    2Qなし―このVIはQを生成しません。Rのサイズはmin(m, n) x nです。
  • i2dcdb.png Q —

    Qは直交行列です。

  • i2dcdb.png R —

    Rは上三角行列です。

  • i2di32.png P —

    Pは、n × nの置換行列です。ここで、n はAの列数です。ピボット?がTRUEの場合にのみ、Pは空ではありません。

  • ii32.png エラー —

    エラーは、VIからのエラーまたは警告を返します。エラーは「エラーコードからエラークラスタ」VIに配線して、エラーコードまたは警告をエラークラスタに変換できます。

    • 以下の式はQR分解を定義します。

    ここで、mは行数、nはAの列数、Qはm x mのユニタリ行列、Rはm x nの上台形行列、R1はk x kの上台形行列です。ここで、kは mとnの最小値、R2はRのm x (n-m) の部分行列、0は (m-n) x nのゼロ行列です。

    QR分解は正方行列の行列式を計算できます。たとえば、以下の式を検証してみます。det(A) = det(Q)*det(R)Qは直交のため、|det(Q)| = 1はTRUEです。したがって、以下もTRUEになります。

    また、 Aが フルランクで m ≧ nのときの連立方程式Ax ＝ bの 最小二乗問題をQR分解で解くことができます。たとえば、以下の式について検証します。

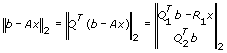
    ここで、以下はTRUEです。

    • Q1のサイズはm x n
    • Q2のサイズはm x (m-n)
    • R1のサイズはn x n

    min(||b – Ax||2) は、min(||Q1Tb – R1x||2) によって異なるため、R1x = Q1Tbの新しい式を解くことにより、解xを求められます。