スプラインインターポラント

PDFをダウンロード

集計された点x[i]でスプラインインターポラント関数g(x)の2次導関数を含む長さｎの配列インターポラントを返します。ここで、i = 0, 1, …, n–1 です。

入力/出力

Y —

Yは、従属値の配列です。Xの要素数がYの要素数と異なる場合、このVIは出力インターポラントを空の配列に設定して、エラーを返します。

X —

Xは、独立値の配列です。Xの要素数がYの要素数と異なる場合、このVIは出力インターポラントを空の配列に設定して、エラーを返します。

初期境界値 —

初期境界値は、x[0]における補間関数g(x)の1次導関数、g'(x[0])です。デフォルトは1.00E+30で、このVIに自然スプライン用に初期境界値条件を設定させます。

g(x)の定義についての詳細は、スプラインインターポラントの詳細を参照してください。

最終境界値 —

最終境界値は、x[n – 1], g'(x[n – 1]) における補間関数g(x)の1次導関数 g'(x[n ? 1]) です。デフォルトは1.00E+30で、このVIに自然スプライン用に最終境界値条件を設定させます。

インターポラント —

インターポラントは、ポイント x[i], i = 0, 1, …, n – 1 における補間関数 g(x) の2次導関数です。

Interpolantを スプライン補間 VIの入力として使用すると、 x₀ ≦ x＜xn_{- 1}の任意の値で yを補間することができます。

エラー —

エラーは、VIからのエラーまたは警告を返します。エラーは「エラーコードからエラークラスタ」VIに配線して、エラーコードまたは警告をエラークラスタに変換できます。

入力配列XおよびYはnの長さで、x₀ < x₁ < … < x_{n - 1}の以下の式に示される表関数を含みます。

f(x_i) = y_i

補間関数g(x) は、以下の公式の区分的関数です。

関数p_i(x)は、以下の条件を満たす必要がある3次多項式です。

g(x_i) = y_i = p_{i(x_i)}
g(x_i) = y_i = p_{i – 1}(x_i)
i = 1, …, n – 2での1および2次導関数で、各内点x_iは連続です。
1. g'(x_i) = p'_i(x_i) = p'_{i - 1}(x_i)
2. g"(x_i) = p"_i(x_i) = p"_{i – 1}(x_i)

3番目の状態では、以下の式が得られます。

ここで、i = 1, …, n – 2を示します。この式では、n – 2の線形方程式はn未知数g"(x_i)に存在します。

「スプラインインターポラント」VIは、以下の式においてx₀およびx_{n – 1}で導関数の2つの式を計算します。

以下の式について検証してください。

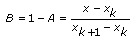
初期境界値は式

最終境界値は式

これらの式では、初期境界値と最終境界値は、それぞれx₀およびx_{n – 1}でのg(x)の最初の微分値です。初期境界値と最終境界値が10³⁰以上の場合、境界値上の2次導関数がなく、自然スプラインに対応する境界値条件をこのVIが設定します。

このVIは、i = 0, 1, …, n – 1の場合のn の式からg"(x_i) を解きます。g"(x_i) はインターポラント出力です。

LabVIEWに含まれている以下のサンプルファイルを参照してください。