Effectue une interpolation unidimensionnelle avec une méthode sélectionnée en fonction de la table de correspondance définie par X et Y.


icon

Entrées/Sorties

  • ci32.png méthode —

    méthode spécifie la méthode d'interpolation.

    0plus proche voisin — Choisit la valeur Y qui correspond à la valeur X la plus proche de la valeur xi actuelle. LabVIEW définit la valeur interpolée au point de données le plus proche.
    1linéaire — Définit les valeurs interpolées à des points le long des segments de ligne connectant les points de données X et Y.
    2spline — Garantit que les dérivées première et seconde des polynômes d'interpolation cubiques sont continues, même aux points de données.
    3Hermite cubique — Garantit que la dérivée première des polynômes d'interpolation cubique est continue et définit la dérivée aux extrémités à des valeurs qui permettent de préserver la forme et la monotonie originales des données Y.
    4Lagrange — Utilise l'algorithme d'interpolation barycentrique de Lagrange.
  • c1ddbl.png Y —

    Y représente le tableau de valeurs tabulées de la variable dépendante.

  • c1ddbl.png X —

    X représente le tableau de valeurs tabulées de la variable indépendante.

    La longueur de X doit être égale à celle de Y.

  • c1ddbl.png xi —

    xi représente le tableau des valeurs de la variable indépendante auxquelles LabVIEW calcule les valeurs interpolées yi de la variable dépendante.

  • cbool.png X est monotone —

    X est monotone spécifie si les valeurs de X augmentent avec l'indice de façon monotone.

    Si X est monotone est VRAI, l'algorithme d'interpolation n'a pas besoin de trier X et de réorganiser Y en conséquence. Si X est monotone est FAUX, ce VI classe les tableaux X en entrée par ordre croissant puis reclasse Y en conséquence.

  • ci32.png n fois —

    n fois détermine les emplacements d'interpolation xi, qui produisent les valeurs interpolées entre les éléments Y lorsque xi est vide. L'interpolation entre les éléments de Y est répétée n fois. Le VI ignore n fois si vous câblez l'entrée xi.

  • i1ddbl.png yi —

    yi renvoie le tableau en sortie des valeurs interpolées qui correspondent aux valeurs de la variable indépendante xi.

  • i1ddbl.png xi utilisé —

    xi utilisé est le tableau 1D de valeurs de la première variable indépendante pour lesquelles il faut calculer les valeurs interpolées de la variable dépendante yi.

    Si xi est vide, xi utilisé renvoie (2ntimes – 1)*(N – 1) + N points, avec (2ntimes – 1) points répartis régulièrement entre deux éléments adjacents de X, N étant la longueur de X. Si vous câblez l'entrée xi, ce VI ignore n fois, et xi utilisé est identique à xi.

  • ii32.png erreur —

    erreur renvoie toute erreur ou mise en garde générée par le VI. Vous pouvez câbler erreur au VI Convertir un code d'erreur en cluster d'erreur pour convertir le code d'erreur ou la mise en garde en cluster d'erreur.

    • Ce VI accepte les valeurs tabulées de variables dépendantes et indépendantes Y et X et renvoie les valeurs interpolées yi qui correspondent à chaque emplacement xi. Ce VI trouve chaque valeur de xi dans X et utilise l'emplacement relatif dans X pour trouver la valeur interpolée yi au même emplacement relatif dans Y.

    Le VI Interpolation 1D vous permet de choisir parmi cinq méthodes d'interpolation. Les sections suivantes contiennent des informations plus détaillées sur chacune de ces méthodes. En lisant ces sections, considérez la situation suivante :

    • X et Y sont déjà en ordre croissant.
    • xj et yj sont respectivement des éléments de X et Y.
    • xim est le m-ième élément de xi, et yim est la m-ième valeur dépendante correspondante de yi.

    Méthode du plus proche voisin

    La méthode du plus proche voisin trouve le point de X le plus proche de xi puis assigne la valeur y correspondante de Y à yi, comme l'illustre le graphe suivant.

    Méthode linéaire

    La méthode linéaire interpole yi sur le segment de ligne qui connecte les deux points (xj, xj + 1) quand xi se trouve entre les deux points (xj, xj + 1) de X, comme l'illustre le graphe suivant.

    Dans le graphe précédent, l'équation suivante est vraie :

    Méthode du spline

    La méthode du spline fait référence à la méthode du spline cubique. Avec cette méthode, le VI dérive un polynôme de troisième ordre pour chaque intervalle entre deux points adjacents. Les polynômes remplissent les conditions suivantes :

    • Les dérivées première et seconde à xj sont continues.
    • Les polynômes passent par tous les points de données spécifiés.
    • Les dérivées secondes sont zéro au début et à la fin.

    Le graphe suivant illustre la méthode du spline cubique.

    Dans le graphe précédent, Pj(x) est le polynôme du troisième ordre entre deux points adjacents, (xj, yj) et (xj + 1, yj + 1).

    Reportez-vous au document A Practical Guide to Splines mentionné dans la rubrique Documentation relative aux mathématiques pour obtenir des informations complémentaires sur la méthode du spline cubique.

    Remarque Si vous choisissez la méthode spline , ce VI renvoie les mêmes résultats que le VI Interpolation Spline 1D avec des conditions limites en spline naturelle.

    Méthode de Hermite cubique

    La méthode du spline de Hermite cubique est l'interpolation de Hermite cubique par morceaux. Cette méthode dérive un polynôme de troisième ordre de forme hermitienne pour chaque intervalle et ne garantit la continuité que pour les dérivées premières des polynômes d'interpolation. La méthode de Hermite cubique a une propriété plus locale que la méthode de spline cubique. Autrement dit, si vous changez un point de données xj, l'effet sur le résultat de l'interpolation se trouve dans la gamme définie par [xj – 1, xj] et [xj, xj + 1].

    Reportez-vous au document A Practical Guide to Splines mentionné dans la rubrique Documentation relative aux mathématiques pour obtenir des informations complémentaires sur la méthode de Hermite cubique.

    Remarque Si vous choisissez la méthode cubique d'Hermite , ce VI renvoie les mêmes résultats que le VI Interpolation d'Hermite 1D .

    Méthode de Lagrange

    La méthode de Lagrange dérive un polynôme d'ordre N – 1 qui passe par tous les N points spécifiés dans X et Y, N étant la longueur de X et Y. Cette méthode est une reformulation du polynôme de Newton qui évite de calculer des différences divisées. L'équation suivante définit la méthode de Lagrange :

    , où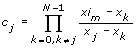

    Pour choisir laquelle des cinq méthodes d'interpolation de ce VI utiliser, les conseils suivants peuvent être utiles :

    • La méthode du plus proche voisin et la méthode linéaire sont simples à utiliser mais ne sont pas assez précises pour la plupart des applications.
    • La méthode du spline renvoie le résultat le plus régulier des cinq méthodes.
    • La méthode de Hermite cubique a une propriété plus locale que les méthodes du spline et de Lagrange.
    • La méthode de Lagrange est d'implémentation facile mais ne convient pas aux calculs exploratoires. La méthode de Lagrange produit un résultat d'interpolation avec des dérivées plus extrêmes que la méthode du spline.

    Exemples

    Reportez-vous aux exemples de fichiers inclus avec LabVIEW suivants.

    • labview\examples\Mathematics\Interpolation\1D Interpolation.vi