Frequency Resolution
- Updated2024-06-07
- 2 minute(s) read
Frequency Resolution
The frequency resolution in a Fast Fourier Transform (FFT) must be fine enough to identify distinct tonal components of the signal independently of the DC value and the noise.
Improving the frequency resolution helps you distinguish two individual tones that are close together. For example, if you analyze a signal that contains two tones at 1,000 Hz and 1,100 Hz, use a sampling frequency of 10,000 Hz. Acquire data for 10 ms with a frequency resolution of 100 Hz. The following figure shows the results of this analysis.
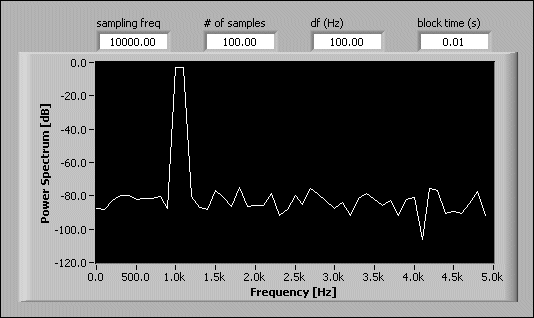
Notice that you cannot distinguish the two tones from one another because the frequency spacing is less than the resolution bandwidth.
Increase the acquisition time to 1 s to achieve a frequency resolution of 1 Hz. The following figure shows the results obtained with a 1 s acquisition time.

You can distinguish the individual tones with the increased acquisition time.
The following strategies achieve a finer frequency resolution:
- Decrease the sampling frequency, fs. Decreasing fs usually is not practical because decreasing fs reduces the frequency range.
- Increase the number of samples, N. Increasing N yields an increased number of lines over the original frequency range.
Implement the decreased fs strategy with zoom FFT analysis. Use baseband FFT and FFT-subset analyses to implement the increased N strategy. Baseband FFT analysis and FFT-subset analysis both achieve the same frequency resolution. However, FFT-subset analysis computes only a narrow subset of the spectrum.