Continuous Frequency Sweep

A chirp signal is a signal whose frequency varies with time. The following figure shows a logarithmic chirp signal, a linear chirp signal, and corresponding frequency profiles.

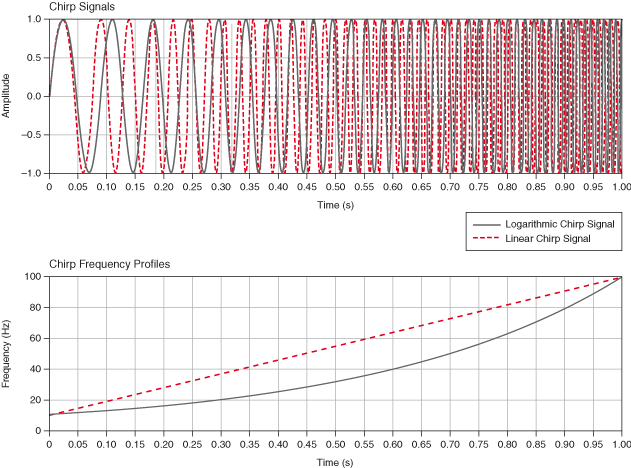
The frequency of the linear chirp signal varies with time linearly. The frequency of the logarithmic chirp signal varies exponentially as a function of time.

You analyze the output of the DUT to acquire swept-sine measurement results, such as the frequency response, distortion, and time waveform of one or multiple harmonics. The following figure shows the process of a continuous swept-sine measurement.

The continuous swept-sine measurement acquires the time-domain response of the DUT under excitation. The time-domain response signal is even-time-spaced. You use the resampling method to convert the time-domain response signal to an even-angle signal. You sample the even-angle response signal at a constant phase-angle interval of the excitation signal. Because you know the phase and time relationship of the excitation signal, you can calculate the signal amplitude at the time instance that corresponds to even-angle positions. You then use the calculated values to form the even-angle signal. The following figure shows the effect of resampling on a chirp signal in a continuous swept-sine measurement.

In the upper-left time signal, as the frequency content of the chirp signal becomes higher, the phase-angle interval between adjacent time samples becomes larger. Accordingly, the period of the signal becomes smaller and the frequency span becomes wider. Identifying the fundamental and harmonic components in the frequency spectrum becomes difficult. In the upper-right even-angle signal, the phase-angle interval between adjacent samples remains constant despite the frequency variation. The period of the even-angle signal is constant. Thus you can apply FFT or filtering to the even-angle signal to extract the fundamental and harmonic components of specified harmonics in the response signal. The magnitude and phase of the fundamental component or the first harmonic component are the frequency response of the DUT. Use the harmonic components to determine whether the DUT produces specific undesired distortion or nonlinear effects.

You can use the same resampling method to convert the even-angle signal to an even-time signal. You can filter out fundamental and harmonic components in angular domain and convert them to time waveforms. Use these time waveforms to perform a sound quality analysis. You also can subtract the fundamental signal from the original time-response signal to detect any residual components in the time-response signal.

The following list describes the advantages of using a continuous swept-sine measurement.

• You can set the frequency range and chirp duration separately to excite the DUT over the test frequency range in the required test duration.
• A continuous swept-sine measurement requires less time than a stepped swept-sine measurement. The chirp signal is phase-continuous, which allows for smooth broadband excitation. Smoother broadband excitation can minimize disturbances and abrupt signal changes to the DUT.
• A continuous swept-sine measurement can produce time waveforms of fundamental, harmonic, or residue components. You can perform a sound quality analysis on the swept-sine measurement results using these time waveforms.
• The sinusoidal chirp signal enables you to perform a simultaneous measurement of the linear response and harmonic distortion.
• You can perform a continuous swept-sine measurement in real-time by processing sequential blocks of data. You can take advantage of the multi-core processing capability that LabVIEW provides for multi-channel computation-intensive applications. You also can perform a continuous swept-sine measurement in one-shot to allow for finite acquisitions and post-processing logged data.