Gaussian Peak Fit VI
- Updated2025-07-30
- 7 minute(s) read
Returns the Gaussian fit of a data set (X, Y) using the Least Square, Least Absolute Residual, or Bisquare method.

Inputs/Outputs
 initial guess
—
initial guess
—
initial guess specifies the initial guesses of amplitude, center, standard deviation, and offset for use in the iterative algorithm. If initial amplitude, initial center, initial standard deviation, or offset is NaN, this VI calculates the initial guess automatically.
 Y
—
Y
—
Y is the array of dependent values. The length of Y must be greater than or equal to the number of unknown parameters.  X
—
X
—
X is the array of independent values. X must be the same size as Y.  Weight
—
Weight
—
Weight is the array of weights for the observations (X, Y). Weight must be the same size as Y. If you do not wire an input to Weight, the VI sets all elements of Weight to 1. If an element in Weight is less than 0, the VI uses the absolute value of the element.  tolerance
—
tolerance
—
tolerance determines when to stop the iterative adjustment of amplitude, center, standard deviation, and offset. For the Least Square and Least Absolute Residual methods, if the relative difference between residue in two successive iterations is less than tolerance, this VI returns the resulting residue. For the Bisquare method, if any relative difference between amplitude, center, standard deviation, or offset in two successive iterations is less than tolerance, this VI returns the resulting amplitude, center, standard deviation, and offset. If tolerance is less than or equal to 0, this VI sets tolerance to 0.0001.  method
—
method
—
method specifies the fitting method.
 parameter bounds
—
parameter bounds
—
parameter bounds contains the upper and lower constraints for the amplitude, center, standard deviation, and offset. If you know the exact value of certain parameters, you can set the lower and upper bounds of the parameters equal to the known values.
 offset
—
offset
—
offset returns the offset of the fitted model.  Best Gaussian Fit
—
Best Gaussian Fit
—
Best Gaussian Fit returns the y-values of the fitted model.  amplitude
—
amplitude
—
amplitude returns the amplitude of the fitted model.  center
—
center
—
center returns the center of the fitted model.  standard deviation
—
standard deviation
—
standard deviation returns the standard deviation of the fitted model.  error
—
error
—
error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.  residue
—
residue
—
residue returns the weighted mean error of the fitted model. If method is Least Absolute Residual, residue is the weighted mean absolute error. Otherwise, residue is the weighted mean square error. |
This VI uses the iterative general Linear Square method and the Levenberg-Marquardt method to fit data to a Gaussian curve in a form described by the following equation:

where x is the input sequence X, a is amplitude, µ is center, σ is standard deviation, and c is offset. This VI finds the values of a, µ, σ, and c that best fit the observations (X, Y).
The following equation specifically describes the Gaussian curve resulting from the Gaussian fit algorithm:

If the noise of Y is Gaussian distributed, use the Least Square method. The following illustration shows the Gaussian fit result using this method.

When you use the Least Square method, this VI finds the amplitude, center, standard deviation, and offset of the Gaussian model by minimizing the residue according to the following equation:

where N is the length of Y, wi is the ith element of Weight, fi is the ith element of Best Gaussian Fit, and yi is the ith element of Y.
The Least Absolute Residual and Bisquare methods are robust fitting methods. Use these methods if outliers in the observations exist. The following illustration compares the fit results of the Least Square, Least Absolute Residual, and Bisquare fitting methods. In most cases, the Bisquare method is less sensitive to outliers than the Least Absolute Residual method.
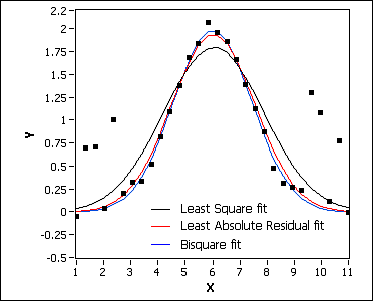
When you use the Least Absolute Residual method, this VI find the amplitude, center, standard deviation, and offset of the Gaussian model by minimizing the residue according to the following equation:

When you use the Bisquare method, this VI obtains the amplitude, center, standard deviation, and offset using an iterative process, as shown in the following illustration, and calculates the residue using the same formula as the Least Square method.
