PID算法
- 更新时间2023-02-21
- 阅读时长3分钟
下列等式说明了基本的PID算法。本章节的信息还包括PID VI实现该算法的方法,以及高级PID算法。
基本PID控制器
下面的模拟程序框图演示了基本PID(比例-积分-微分)控制器:

 |
注: 创建类似上面的模拟程序框图需要LabVIEW Control Design and Simulation模块。但借助PID VI可实现PID控制器。用户无需Control Design and Simulation模块便可生成PID控制器。 |
误差计算(e)
PID控制器通过比较设定值(SP)和过程变量(PV)获得误差(e),如下所示:

| 其中 | e表示误差 |
| SP表示设定值 | |
| PV表示过程变量 |
控制器操作(u(t))
PID控制器计算控制器操作u(t),方法如下:
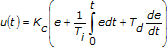
| 其中 | Kc表示控制器增益 |
| Ti表示积分时间(单位为分钟),也称重置时间 | |
| Td表示微分时间(单位为分钟),也称比率时间 |
该等式包含三个同时应用到控制器输出的操作:
比例操作(P)
比例操作(P)与误差(e)成比例。该项定义了控制器必须响应误差改动的速度。下面的公式表示比例操作:

积分操作(I)
积分操作(I)与误差(e)积分成比例。该项一般用于更正稳态误差并避免系统中出现干扰。下面的公式表示积分操作:
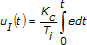
微分操作(D)
微分操作(D)与误差(e)微分成比例。该项用于制动响应,避免系统发生过冲。下面的公式表示微分操作:
