入力シーケンスXの実ウォルシュ･アダマール変換を計算します。


icon

入力/出力

  • c1ddbl.png X —

    Xは2の累乗の長さの配列です。

  • i1ddbl.png ウォルシュ・アダマール{X} —

    ウォルシュ・アダマール{X}は、Xのウォルシュ・アダマール変換を返します。

  • ii32.png エラー —

    エラーは、VIからのエラーまたは警告を返します。エラーは「エラーコードからエラークラスタ」VIに配線して、エラーコードまたは警告をエラークラスタに変換できます。

    • メモ ウォルシュ・アダマール変換にはよく知られているフーリエ変換に類似した属性がありますが、計算のコストは比較的に小さくなります。

    ウォルシュ・アダマール変換は、-1と1の要素の関数で構成される直交性システムに基づきます。n = 4の特別な場合、信号

    X = {x0, x1, x2, x3}

    のウォルシュ・アダマール変換は、以下の行列形式で示すことができます。

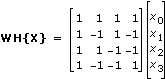
    WHnおよびWHn + 1が、それぞれ次元2nと2n + 1のウォルシュ・アダマール行列を表す場合、以下の公式で示されます。

    ,

    ここで、–WHnは要素に関連します。

    メモ ウォルシュ・アダマール変換は、コンボリューション理論 (WH{X*Y} = WH{X}WH{Y}) の条件を満たします。

    以下のダイアグラムは、長さ256、遅延32、幅64のパルスパターン信号のウォルシュ・アダマール変換を示します。