指定された開始条件で、微分方程式の n 次の線形システムを解きます。解は、行列にある固有値と固有ベクトルに基づいています。解は記号形式で求められます。


icon

入力/出力

  • c2ddbl.png A (係数の行列) —

    Aは、線形システムを表すn x n行列です。

  • c1ddbl.png X0 (開始値) —

    X0は、開始条件 x[10], …, x[n0] を示すn ベクトルです。

    X0とXの要素間は1対1の関係です。

  • istr.png フォーミュラ —

    フォーミュラは、LabVIEWの標準フォーミュラ表記法にある線形システムの解を含む文字列です。解ベクトルの要素は、復帰文字で区切られます。

  • ii32.png エラー —

    エラーは、VIからのエラーまたは警告を返します。X、X0、および、F(X,t)の入力に不正確な値を使用すると、エラーが発生します。エラーは「エラーコードからエラークラスタ」VIに配線して、エラーコードまたは警告をエラークラスタに変換できます。

    • メモ このVIは、反復する固有値、複素共役固有値などがある実行列Aのほとんどすべてのケースで正しく動作します。例外は、特異固有ベクトル行列のケースです。これは、固有ベクトルが空間全体にスパンしない行列です。固有ベクトル行列が特異である場合、-23016のエラーが発生します。

    このシステムで表される線形微分方程式で

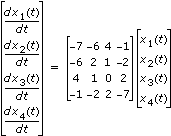
    と

    x1(0) = 1 x2(0) = 2 x3(0) = 3 x4(0) = 4

    解は以下のようになります。

    + 1.62*e(-12.46*t) - 1.28*e(-6.30*t) + 0.63*e(1.34*t) + 0.04*e(5.42*t) + 0.84*e(-12.46*t) - 0.29*e(-6.30*t) + 1.51*e(1.34*t) - 0.06*e(5.42*t) -0.73*e(-12.46*t) + 0.01*e(-6.30*t) + 3.69*e(1.34*t) + 0.02*e(5.42*t) + 0.87*e(-12.46*t) + 2.67*e(-6.30*t) + 0.45*e(1.34*t) + 0.01*e(5.42*t)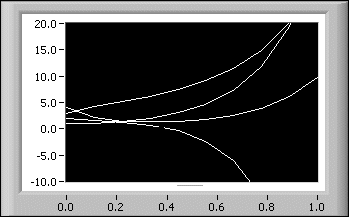

    以下のパラメータリストは、フロントパネルに以前の式を入力する方法を示します。

    • A: [-7, -6, 4, 1; -6, 2, 1, -2; 4, 1, 0, 2; -1, -2, 2, -7]
    • X0: [1, 2, 3, 4]