指定された開始条件で、定数係数を持つ n 次で同一の線形微分方程式を解きます。


icon

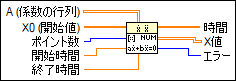
入力/出力

  • c2ddbl.png A (係数の行列) —

    Aは、線形システムを表すn x n行列です。

  • c1ddbl.png X0 (開始値) —

    X0は、開始条件 x[10], …, x[n0] を示すn ベクトルです。

    X0とXの要素間は1対1の関係です。

  • cu32.png ポイント数 —

    ポイント数は開始時間と終了時間の間の等距離時間ポイントの数です。デフォルトは10です。

  • cdbl.png 開始時間 —

    開始時間はODEの開始ポイントです。デフォルトは0です。

  • cdbl.png 終了時間 —

    終了時間は、調査対象の時間間隔の終了ポイントです。デフォルトは1.0です。

  • i1ddbl.png 時間 —

    時間は時間ステップを表す配列です。この方法は、開始時間と終了時間の間の等距離時間ステップを求めます。

  • i2ddbl.png X値 —

    X値は、等距離時間ポイントにおける解Xの行列です。

  • ii32.png エラー —

    エラーは、VIからのエラーまたは警告を返します。X、X0、および、F(X,t)の入力に不正確な値を使用すると、エラーが発生します。エラーは「エラーコードからエラークラスタ」VIに配線して、エラーコードまたは警告をエラークラスタに変換できます。

    • VIの解は、行列Aにある固有値と固有ベクトルに基づいています。解は数値形式で求められます。

    メモ このVIは、反復する固有値、複素共役固有値などがある実行列Aのほとんどすべてのケースで正しく動作します。例外は、特異固有ベクトル行列のケースです。これは、固有ベクトルが空間全体にスパンしない行列です。固有ベクトル行列が特異である場合、-23016のエラーが発生します。

    線形システムは以下の示すとおりです。

    X(0) = X0

    開始時間 = 0の場合、

    ここでは

    X(t) = (x0(t), …, xn(t))

    Aは、n x n の実行列です。線形システムは、Aの固有値と固有ベクトルの決定により解が求められます。S を n 次元空間全体をスパンするすべての固有ベクトルのセットとします。変換 Y(t) = SX(t) により以下のとおりになります。

    Y(0) = SX0

    行列 SAS–1 には対角行列のため解は明らかです。解 X(t) は逆変換によって決まります。

    X(t) = S–1Y(t)
    メモ 基本操作は行列Aの固有ベクトルと固有値の計算であるため、ティック出力は実装されません。この操作はAの比較的小さい次元では無視できます。

    以下の図は、以下のシステムにより表される線形微分方程式の解の4つのコンポーネントを示します。

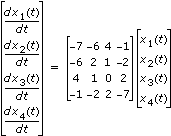
    と

    x1(0) = 1 x2(0) = 2 x3(0) = 3 x4(0) = 4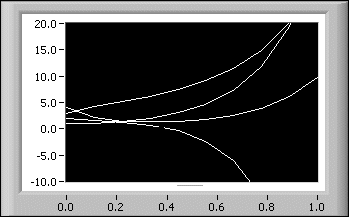

    以下のパラメータリストは、フロントパネルに以前の式を入力する方法を示します。

    • A: [-7, -6, 4, 1; -6, 2, 1, -2; 4, 1, 0, 2; -1, -2, 2, -7]
    • X0: [1, 2, 3, 4]
    • 開始時間: 0.00
    • 終了時間: 1.00