オイラー法を使用して、初期状態で常微分方程式を解きます。


icon

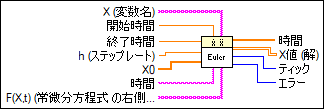
入力/出力

  • c1dstr.png X (変数名) —

    Xは変数の文字列の配列です。

  • cdbl.png 開始時間 —

    開始時間はODEの開始ポイントです。デフォルトは0です。

  • cdbl.png 終了時間 —

    終了時間は、調査対象の時間間隔の終了ポイントです。デフォルトは1.0です。

  • cdbl.png h (ステップレート) —

    hは固定ステップレートです。デフォルトは 0.1 です。

  • c1ddbl.png X0 —

    X0は、開始条件 x[10], …, x[n0] のベクトルです。

    X0とXの要素間は1対1の関係です。

  • cstr.png 時間 —

    時間は時間変数を表す文字列です。デフォルトの変数はtです。

  • c1dstr.png F(X,t) (常微分方程式 の右側はXとtの関数) —

    F(X,t)は、微分方程式の右辺を表す文字列の1次元配列です。フォーミュラでは有効な変数をいくつでも使用できます。

  • i1ddbl.png 時間 —

    時間は時間ステップを表す配列です。オイラー法は、開始時間と終了時間の間の等距離時間ステップを求めます。

  • i2ddbl.png X値 (解) —

    X値は解ベクトルx[10]、 …、x[n] の2D配列です。

    最上位指標は時間配列で指定されたように時間ステップを実行し、最下位指標はx[10]、…、x[n]の要素を実行します。

  • iu32.png ティック —

    ティックは、関数値の全体の計算に要する目標時間 (ミリ秒) です。

  • ii32.png エラー —

    エラーは、VIからのエラーまたは警告を返します。X、X0、および、F(X,t)の入力に不正確な値を使用すると、エラーが発生します。エラーは「エラーコードからエラークラスタ」VIに配線して、エラーコードまたは警告をエラークラスタに変換できます。

    • 常微分方程式 (ODE) の一般的な形式は以下のとおりです。

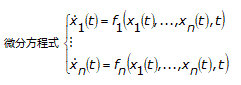
    と

    関数f1, …, fn、数値、開始ポイントt = t0が指定されています。F = (f1, …, fn); X(t) = (x1(t), …, xn(t)); および X0 = (x10, …, xn0)の規約を使用して、

    以下を得ることができます。

    上記の式を満たす関数Xを決定する必要があります。

    オイラー法は最も基本的な方法で、ODEを解くのに役に立つ方法です。t0および固定ステップレートh (通常は比較的小さい値) で開始すると、以下の式によって、新規値

    X（t 0＋ h）＝ X（t0）＋hF（X（t0）， t）。 X(t0 +2h) = X(t0 + h) +hF(X(t0 + h),t0 + h) ⋮

    が計算されます。この処理は、 time start +nh ≧ time end、ここで time endは 調査対象の時間間隔の右終点である場合に停止する。

    以下の図は、以下の常微分方程式の解を示します。

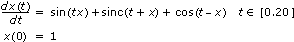
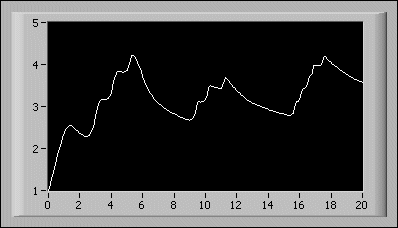
    上記の式と初期状態は、以下のようにフロントパネルに入力されます。

    • 開始時間: 0.00
    • 終了時間: 20.00
    • X0: 1.00
    • F(X,t): sin(t*x) + sinc(t + x) + cos(t - x)
    • X: x