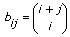特殊複素行列を作成
- 更新日2025-07-30
- 5分で読める
行列タイプに基づいて特殊行列を生成します。入力ベクトル2入力と入力ベクトル1入力に配線するデータタイプによって、使用する多態性のインスタンスが決まります。

入力/出力
 入力ベクトル2
—
入力ベクトル2
—
入力ベクトル2は、一部のオプションでは、特殊行列を構成する入力として使用されます。  行列タイプ
—
行列タイプ
—
行列タイプは、特殊行列出力の生成に使用される特殊行列のタイプを指定します。 nは行列サイズ、Xは入力ベクトル1、nxはXのサイズ、Yは入力ベクトル2、nyはYのサイズ、Bは出力特殊行列を表すものとします。
 行列サイズ
—
行列サイズ
—
行列サイズは、出力特殊行列の次元サイズを指定します。  入力ベクトル1
—
入力ベクトル1
—
入力ベクトル1は、一部のオプションでは、特殊行列を構成する入力として使用されます。  特殊行列
—
特殊行列
—
特殊行列は生成される行列です。  エラー
—
エラー
—
エラーは、VIからのエラーまたは警告を返します。エラーは「エラーコードからエラークラスタ」VIに配線して、エラーコードまたは警告をエラークラスタに変換できます。 |
サンプルプログラム
LabVIEWに含まれている以下のサンプルファイルを参照してください。
- labview\examples\Mathematics\Linear Algebra\Matrix to a Power.vi