3D ANOVA
- 更新日2025-07-30
- 13分で読める
3つの因子の異なる水準での実験観測値の配列を使用して、3元配置分散分析を実行します。

入力/出力
 水準
—
水準
—
水準は、A、B、C因子 (固定または不規則) の効果と同様に、A、B、C因子の水準数に対応する3つの数値のクラスタです。
 X
—
X
—
Xには、すべての観測データが含まれています。  指標A
—
指標A
—
指標Aには、該当する観測値が属する因子Aの水準が含まれています。  指標B
—
指標B
—
指標Bには、該当する観測値が属する因子Bの水準が含まれています。  指標C
—
指標C
—
指標Cには、対応する観測値が属する因子Cの水準が含まれています。  観測数/セル
—
観測数/セル
—
観測数/セルは、各セル内の観測数です。これは、すべてのセルに対して同じです。  情報
—
情報
—
情報は、最初の列が因子 (A、B、C)、相互作用 (AB、AC、BC、ABC)、残差誤差に関連付けられた二乗の和に対応するように構成された、8 x 4 の行列です。 2番目の列は、その自由度に対応します。 3番目の列は、その二乗平均に対応します。 4番目の列は、そのF値に対応します。   有意水準
—
有意水準
—
有意水準は、有意性水準に対応する7つの数値のクラスタです。
 エラー
—
エラー
—
エラーは、VIからのエラーまたは警告を返します。エラーは「エラーコードからエラークラスタ」VIに配線して、エラーコードまたは警告をエラークラスタに変換できます。 |
ANOVAでは、因子または因子間の相互作用が実験結果に大きく影響する証拠を求めます。モデル間での相違点は、この操作を実行するメソッドにあります。
3D ANOVA変量効果と固定効果
結論を引き出すために使用する水準の数が多く、すべての水準からサンプルできない場合、因子は変量効果です。したがって、ランダムに水準を選択して、すべての水準の一般化を求めます。結論を出すために使用するすべての水準からサンプルできる場合、因子は固定効果です。
3D ANOVA統計モデル
xpqrsは、Aのp番目の水準、Bのq番目の水準、r番目の水準におけるs番目の観測値であるとします (s = 0, 1, ..., L– 1)。各観測値を8つの構成部分の和として表します。したがって、フォーミュラは以下のようになります。
xパークス = µ + αp + βq + γr + (αβ)pq + (αγ)プリ + (βγ)qr + (αβγ)ピーアール + εパークスここで、
- μは総合平均です。
- αp は、要因Aのp 番目のレベルの平均的な効果である。
- βq は、q 番目のレベルの要因Bの平均効果である。
- γr は、 第r 階層の要因 C の平均効果である。
- (αβ)pq は、因子Aのp 番目のレベルと因子Bのq 番目のレベルとの2因子相互作用である。
- (αγ)プリ は、因子Aのp 番目のレベルと因子Cのr 番目のレベルとの2因子相互作用である。
- (βγ)qr は、因子Bのq 番目のレベルと因子Cのr 番目のレベルの2因子相互作用である。
- (αβγ)ピーアール は、因子Aのp 番目のレベル、因子Bのq 番目のレベル、因子Cのr 番目のレベルの3因子の相互作用である。
- εパークス はランダムな揺らぎである。
3D ANOVAの仮説
以下の各仮説は、因子または因子間の相互作用は実験結果への影響がないことを異なる方法で示します。このVIは、作用がないことを想定して、これらの仮定説を否定する証拠を求めます。以下は、7つの仮説の例です。
- (というαp 要因Aが固定であれば、すべてのレベル pについて =0であり、要因Aがランダムであれば、σA²=0である。
- (になるように、βq 要因Bが固定であれば、すべてのレベル qについて =0であり、要因Bがランダムであれば、σB²=0である。
- (C)であることをγr 要因Cが固定であれば、すべてのレベル rに対して =0であり、要因Bがランダムであれば、σC²=0であること。
- (AB)であること(αβ)。pq 因子AおよびBが固定であれば、すべてのレベル p および qについて =0であり、因子AまたはBのいずれかがランダムであれば、σAB² = 0である。
- (AC) その(αγ)。プリ 因子AおよびCが固定であれば、すべてのレベル p および qについて =0であり、因子AまたはCのいずれかがランダムであれば、σAC² = 0である。
- (その(βγ)こと)qr 因子BとCが固定であれば、すべてのレベル pと qについて =0であり、因子BとCのどちらかがランダムであれば、σBC² = 0である。
- (ABC)であること(αβγ)。ピーアール 因子A、B、Cが固定であれば、すべてのレベル p、 q、 rについて =0であり、因子A、B、Cのいずれかがランダムであれば、σABC²=0となる。
3D ANOVAにおける前提
「3D ANOVA」VIでは、以下を仮定します。
- 各p、 q、 rについて、εを仮定する。パークス は平均0、分散σe²で正規分布する。
- 因子Aを固定した場合、Aの各レベルにおける測定値の母集団が平均αで正規分布すると仮定する。p + μ、分散σA²であり、各水準のすべての集団が同じ分散を持つこと。また、αを想定してp の合計がゼロになる。BとCに対しても、同じ推測を行います。
- 要因Aがランダムである場合、A自体のレベルの効果αを想定する。pは、平均0、分散σA²で正規分布する確率変数である。BとCに対しても、同じ推測を行います。
- 交互作用の効果に関連するAやBなどの因子の一部が(αβ)である場合pq を固定し,A,Bの各レベルにおける測定値の母集団が平均μ+αで正規分布していると仮定する。p + βq + (αβ)pq と分散σAB²があります。任意の固定 pに対して、平均値(αβ)はpq は、すべての qについて合計するとゼロになる。同様に、任意の固定 qについて、(αβ)pq は、すべての pについて合計するとゼロになる。
- 交互作用(αβ)の効果に関連するA、Bなどの因子のいずれかがあればpq はランダムであり、効果は平均0、分散σAB²で分布するランダム変数Normallyであると仮定する。Aが固定でBがランダムな場合、任意の固定 qに対して、平均値(αβ)を仮定する。pq は、すべての pについて合計するとゼロになる。同様に、Bは固定だがAはランダムである場合、任意の固定 pについて 、平均値(αβ)を仮定する。pq は、すべての qについて合計するとゼロになる。
- 確率変数として使用されるすべての効果は互いに独立していることを仮定します。
3D ANOVAの一般的な方法
各モデルにおいて、VIは全集合平均からのデータの総変動の基準となる2乗総和 (tss) を2乗成分和の特定の数値に分解します。
tss = ssa + ssb + ssc + ssab + ssac + ssbc + ssabc + ssetssの和の各構成要素は、特定の因子または因子間での相互作用に帰する変動の基準です。ここで、ssaは因子Aに帰する変動の基準、ssbは因子Bに帰する変動の基準、sscは因子Cに帰する変動の基準、ssabは因子AとB間の相互作用に帰する変動の基準などとなり、ssac、ssbc、ssabcに対しても同様です。また、sseは、変量変動に帰する変動の基準です。VIは各構成要素をそれぞれの自由度で除算することによって、msa、msb、msc、msab、msac、msbc、msabc、mseの対応する平均値を求めます。たとえば、因子Aが実験観測値に大きく影響する場合、msaの値は比較的大きくなります。
3D ANOVAの仮説を検定する
各仮説では、VIは、関連付けられたSig確率の計算に使用される数値fを計算します。たとえば、仮説(A)の場合、VIが計算するすべての水準p (固定A) に対してp = 0となります。

ならば
sigA = Prob{Fa – 1, abc(L – 1) > fa}ここで、
Fa – 1, abc(L – 1)は、自由度がa – 1およびabc(L – 1)のF分布です。さらに、確率sigA、sigB、sigC、sigAB、…、sig ABCを使用して、関連付けられた仮説 (A)、(B)、(C)、(AB)、…、(ABC)を拒否するタイミングを指定できます。
帰無仮説を却下すべき場合を判断するには、仮説ごとに有意性水準を選択します。この有意性水準は、仮説を誤って却下する確率です (一般に0.05が選択されます)。選択した有意性水準を関連付けられたSig確率の出力値と比較します。Sig確率が選択した有意性水準よりも低い場合、帰無仮説を却下してください。例えば、Aがランダム効果で、有意水準が0.05で、 sigA = 0.03の場合、σA²= 0という仮説を棄却し、要因Aが実験観察に効果があると結論づけなければならない。
一部のモデルでは、特定の仮説に対する適切なテストはありません。このような場合、これらの仮説の検定に直接必要となる出力パラメータは–1.0です。
3D ANOVAフォーミュラ
xpqrsは、Aのp番目の水準、Bのq番目の水準、r番目の水準におけるs番目の観測値であるとします (s = 0, 1, ..., L – 1)。
計算式は、次のとおりです。
a = |A水準|
b = |B水準|
c = |C水準|
ならば
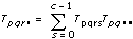
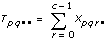
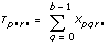
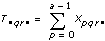

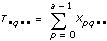
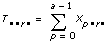
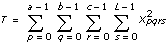

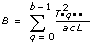
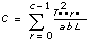





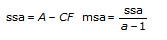
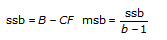
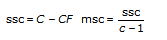
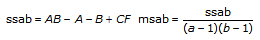


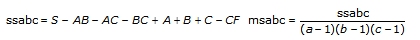
 sig A
—
sig A
—