1D ANOVA
- 更新日2025-07-30
- 8分で読める
因子の異なる水準で行われる実験的観測の配列Xを使用して、最低各水準につき1回の観測を行う割合で、固定効果モデルで1元配置分散分析を実行します。

入力/出力
 X
—
X
—
Xには、すべての観測データが含まれています。  指標
—
指標
—
指標には、対応する観測値が属する水準が含まれています。  水準数
—
水準数
—
水準数は水準の総数です。  f
—
f
—
fは、f = msa/mseの比率です。  ssa
—
ssa
—
ssaは、因子に起因する変動の基準です。  sse
—
sse
—
sseは、不規則変動に起因する変動の基準です。  mse
—
mse
—
mseは、sseに関連する平均二乗です。これは、sseをその自由度で除算して求められます。  msa
—
msa
—
msaは、ssaに関連する平均平方です。これは、ssaをその自由度で除算して求められます。  tss
—
tss
—
tssは、母集団全体の平均からのデータの総変動の基準である総平方和です。これは、tss = ssa + sseを使用して計算されます。  エラー
—
エラー
—
エラーは、VIからのエラーまたは警告を返します。エラーは「エラーコードからエラークラスタ」VIに配線して、エラーコードまたは警告をエラークラスタに変換できます。  sig A
—
sig A
—
特定のfがあると仮定した場合、sig Aは、F分布からサンプリングする場合、fよりも大きい値が抽出される確率です。 |
1元配置分散分析では、VIは因子の水準が実験結果に影響を及ぼすかどうかをテストします。
1D ANOVAの因子と水準
因子とは、データを分類するための基準です。たとえば、個人の腹筋回数をカウントする場合、分類基準の1つは年齢です。年齢の場合、以下の水準に分類できます。
| 水準0 | 6歳~10歳 |
| 水準1 | 11歳~15歳 |
| 水準2 | 16歳~20歳 |
ここで、観測のセットを実行して、腹筋を何回繰り返すことができるかを調べます。5人のサンプルをランダムに選択した場合、以下の結果が生成される可能性があります。
| 対象1 | 8歳 (水準0) | 10回の腹筋 |
| 対象2 | 12歳 (水準1) | 15回の腹筋 |
| 対象3 | 16歳 (水準2) | 20回の腹筋 |
| 対象4 | 20歳 (水準2) | 25回の腹筋 |
| 対象5 | 13歳 (水準1) | 17回の腹筋 |
各水準ごとに最低1回の観測が実行されたことに注目してください。分散分析を実行するには、各水準につき最低1回の観測を行う必要があります。
分散分析を実行するには、観察の配列Xに10、15、20、25、17の値を指定します。配列指標は、各観測値が適用される水準 (またはカテゴリ) を指定します。この場合、指標は0、1、2、2、1の値になります。最後に、3つの水準が可能であるため、水準数パラメータに3の値を渡します。
1D ANOVA統計モデル
分散分析を実行して、各実験結果を3つの構成部分として表します。ximをi 番目のレベルからのm番目の観測値とします。各観測値は、以下のように表わされます。
キシム =μ+αi + εイムここで、μは総合平均と呼ばれる標準の効果です。
αiは 、第i 水準の要因の効果であり、第i 水準の平均値αとの差である。i と全体の平均値
μ(ミューi) = µ + αiとεイム はランダムな揺らぎである。
1D ANOVAの仮説
このVIでは、αi = i = 0, 1, ..., k - 1、ここで kは レベルの数である。つまり、帰無仮説と呼ばれるこの仮説は、水準は実験結果に影響しないとして、反証を求めます。
1D ANOVAにおける前提
各レベルの測定値の母集団が平均μの正規分布であると仮定する。i と分散σA²を仮定し、αi の合計がゼロになる。最後に、 各iと mについて、εを仮定する。イム は平均0、分散σA²で正規分布する。
1D ANOVAの一般的方法
このVIは、全個体郡の平均からのデータの全変動の基準となる2乗総和 (tss) です。
tssは、因子に起因する変動を表すssaおよび変量変動に起因する変動を表すsseの2つの部分から構成されます。つまり、以下のような関係が成り立ちます。
tss = ssa + sseVIは、ssaとsseをそれぞれの自由度で除算することによって、ssaとsseから2つの二乗平均値msaとmseを計算します。mseに対するmsaの比率が大きいほど、因子による実験結果への影響が大きくなります。
特に、帰無仮説が真の場合、比率f (f = msa/mse) は、自由度がk–1と n–k であるF分布から抽出されます。この比率から、確率を求めることができます。特定のfに関して、sigAは、この分布からサンプリングした場合にfよりも大きい値が得られる確率です。
1D ANOVAの仮説をテストする
帰無仮説を誤って却下する確率を決定することで、帰無仮説を却下するタイミングを決定します。これは有意性水準で、通常0.05が選択されます。出力sigAは選択された有意性水準と比較されて、帰無仮説の成否を決定します。選択された有意性水準よりもsigAが低い場合は、帰無仮説を却下してください。帰無仮説を却下する場合、最低1つのレベルが実験結果にある程度の影響を及ぼすことを認識する必要があります。
1D ANOVAフォーミュラ
ximは、m = 0, 1, …, ni – 1、i = 0, 1, …, k– 1の場合でのi番目の水準におけるm番目の観測値とします。ni はi番目の水準での観測値の数、k は水準数です。
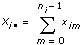
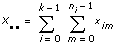
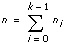
ならば
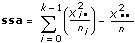
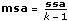
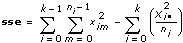

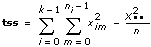

SigA = Prob{Fk – 1, n – k > f}
Fk – 1, n – k
は、自由度がk –1 および n –k のF分布です。
サンプルプログラム
LabVIEWに含まれている以下のサンプルファイルを参照してください。
- labview\examples\Mathematics\Probability and Statistics\Unbalanced ANOVA on Rainfall Data.vi