実逆FFT
- 更新日2025-07-30
- 5分で読める
入力シーケンスFFT {X}の逆離散フーリエ変換 (DFT) を計算します。使用する多態性インスタンスを手動で選択する必要があります。

入力/出力
 FFT{X}
—
FFT{X}
—
FFT {X}は複素値入力シーケンスです。これは、最初の要素を除いて、中心対象に共役転置されます。このインスタンスはFFT {X}の前半分のみを使用します。  シフト?
—
シフト?
—
シフト?は、DC成分がFFT {X}の中央にあるかどうかを指定します。デフォルトはFALSEです。  X
—
X
—
XはFFT {X}の実逆FFTです。  エラー
—
エラー
—
エラーは、VIからのエラーまたは警告を返します。エラーは「エラーコードからエラークラスタ」VIに配線して、エラーコードまたは警告をエラークラスタに変換できます。 |
このVIの実数逆FFTおよび2D実数逆FFTインスタンスは、FFT {X}が実時間領域信号実フーリエ変換の場合のみに使用します。それ以外の場合は、複素逆FFTおよび2D複素逆FFTインスタンスを使用します。FFT {X}が実数のフーリエ変換の時間領域信号である場合、FFT {X}は中心対象に共役転置され、実数逆FFTと2D実数逆FFTのインスタンスではFFT {X}の前半分のみを使用します。
以下の式は、FFT {X}が実数のフーリエ変換の時間領域信号でシフト?がFALSEの場合、FFT {X}の中心対象の共役転置のプロパティを示します。
-
FFT {X}が長さ N の1Dのフーリエ変換の実数時間領域信号である場合、FFT {X}の後半分は前半分で構成できます。FFT {X}の前半分と後半分の中心対象関係は以下のように記述できます。
 、
、ここで、fi はFFT {X}の要素です。
「実逆FFTインスタンス」VIはf0からf_
 までの前半分のみを使用し、実逆FFTを実行します。ここで、
までの前半分のみを使用し、実逆FFTを実行します。ここで、 はフロア演算です。
はフロア演算です。 -
FFT {X}が M 行と N 列の2Dの実数時間領域信号のフーリエ変換である場合、FFT {X}の下半分は上半分で構成できます。FFT {X}の上半分と下半分の中心対象関係は以下のように記述できます。

ここで、fi,j はFFT {X}の要素です。
2D実逆FFTインスタンスはf0.0からf_
 までの上半分のみを使用し、2D実逆FFTを実行します。ここで、
までの上半分のみを使用し、2D実逆FFTを実行します。ここで、 はフロア演算です。
はフロア演算です。
このVIは、行列FFT {X}またはベクトル逆離散フーリエ変換 (IDFT) を高速フーリエ変換アルゴリズムを計算します。シフト?入力は、入力FFT {X}がDC中心のFFTであるかどうかを指定します。
1Dの場合、N-サンプル、周波数領域シーケンスY、IDFTは以下のように定義されます。
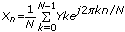
ここで、n=0, 1, 2,…, N–1 です。
1Dの場合、M-x-N 周波数領域配列 Y、IDFTは以下のように定義されます。
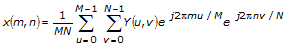
ここで、 m = 0, 1, …, M–1, n=0, 1, …, N–1 です。