Détermine la solution d'un problème de programmation linéaire.


icon

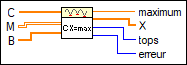
Entrées/Sorties

  • c1ddbl.png C —

    C est un vecteur décrivant la fonction linéaire à maximiser.

  • c2ddbl.png M —

    M est une matrice décrivant les différentes contraintes.

  • c1ddbl.png B —

    B est un vecteur décrivant les membres de droite des inégalités de contraintes.

  • idbl.png maximum —

    maximum est la valeur maximale, si elle existe, de x sous les contraintes.

  • i1ddbl.png X —

    X est le vecteur solution.

  • iu32.png tops —

    tops est le temps, en millisecondes, consacré à la totalité du calcul.

  • ii32.png erreur —

    erreur renvoie toute condition d'erreur ou de mise en garde du VI. La non-existence d'une solution X donne lieu à une erreur. Vous pouvez câbler erreur au VI Convertir un code d'erreur en cluster d'erreur pour convertir le code d'erreur ou la mise en garde en cluster d'erreur.

    • La formule suivante définit le problème d'optimisation résolu par ce VI.

    cx = max!

    avec les contraintes x ≥ 0 et mx ≥ b.

    Pour le problème d'optimisation cx = max!, utilisez les définitions suivantes :

    X =(x1, ..., xn) C =(c1, ..., cn) B =(b1, ..., bk) M est une matrice kpar n.

    Pour résoudre le problème d'optimisation, vous devez décider s'il existe un vecteur optimal X. Si ce vecteur X existe, vous devez le déterminer.

    La résolution d'un problème de programmation linéaire est un processus à deux étapes. Suivez les étapes suivantes pour résoudre un problème de programmation linéaire.

    1. En premier lieu, convertissez le problème d'origine en un problème sous forme normale restreinte, essentiellement sans inégalités dans la formulation.
    2. Résolvez la forme normale restreinte du problème.
    Remarque La formulation normale restreinte semble spéciale au premier abord. Mais il existe de nombreuses façons de reformuler les termes. Par exemple, dx ≤ e est équivalent à-dx ≥ -e et, dx = e est équivalent à la combinaison dx ≥ e et-dx ≥ -e.

    Exemples

    Reportez-vous aux exemples de fichiers inclus avec LabVIEW suivants.

    • labview\examples\Mathematics\Optimization\Geometrical Analysis with Linear Programming.vi