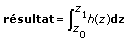Effectue une intégration numérique sur le Tableau en entrée en utilisant une des quatre méthodes d'intégration numérique couramment utilisées. Câblez des données à l'entrée Tableau en entrée pour déterminer l'instance polymorphe à utiliser ou sélectionnez manuellement l'instance.


icon

Les valeurs de x que vous câblez à ce VI doivent être espacées de manière uniforme pour que le résultat soit correct. Si les valeurs ne sont pas espacées régulièrement, vous pouvez utiliser le VI Intégration numérique inégale pour calculer l'intégrale.

Intégration numérique 1D

Nombre de pointsÉvaluations partielles effectuées
22455 Bode, 1 Simpsons 3/8
22556 Bode
22656 Bode, Trapézoïdale
22756 Bode, 1 Simpsons
22857 Bode, 1 Simpsons 3/8

Si 224 points ont été fournis et que la méthode de Bode a été choisie, le VI obtiendra le résultat en effectuant 55 évaluations par la méthode de Bode et une évaluation par la méthode de Simpsons 3/8.

Chacune de ces méthodes dépend de l'intervalle d'échantillonnage (dt) et calcule l'intégrale en utilisant des applications successives d'une formule de base pour effectuer des évaluations partielles qui dépendent d'un certain nombre de points adjacents. Le nombre de points utilisés dans chaque évaluation partielle représente l'ordre de la méthode. Le résultat est la somme de ces évaluations partielles successives.

où j est une gamme qui dépend du nombre de points et de la méthode d'intégration.

Les formules de base pour le calcul de la somme partielle de chaque règle, par ordre croissant de méthode, sont :

  • Trapézoïdale : 1/2(x[i] + x[i + 1])*dt
  • Simpsons : (x[2i] + 4x[2i + 1] + x[2i + 2])*dt/3, k = 2
  • Simpsons 3/8 : (3x[3i] + 9x[3i + 1] + 9x[3i + 2] + 3x[3i + 3]) * dt/8, k = 3

  • Bode : (14x[4i] +64x[4i + 1] +24x[4i + 2] +64x[4i + 3] +14x[4i + 4]) * dt/45, k = 4

    pour i = 0, 1, 2, 3, 4, ..., Partie Intégrale de [(N - 1)/k]

où N est le nombre de points de données, k est un entier dépendant de la méthode et x est le tableau en entrée.

Remarque Si le nombre de points fournis pour une certaine méthode choisie ne contient pas un nombre entier de sommes partielles, la méthode est appliquée pour tous les points possibles. Pour les points restants, la prochaine méthode possible d'ordre inférieur est utilisée. Par exemple, si la méthode de Bode est sélectionnée, l'exemple précédent montre ce que ce VI évalue pour différents nombres de points.

Intégration numérique 2D

Pour effectuer une intégration numérique 2D de

,

ce VI applique d'abord une intégration numérique 1D sur x pour évaluer

.

Ensuite, ce VI applique une intégration numérique 1D sur y pour obtenir le résultat

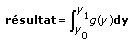
Intégration numérique 3D

Pour effectuer une intégration numérique 3D de

,

ce VI applique une intégration numérique 1D sur x, y, et z, à la suite, comme illustré dans les équations suivantes :