Factorisation en LU d'une matrice réelle
- Mise à jour2025-07-30
- Temps de lecture : 3 minute(s)
Effectue la factorisation en LU de A de telle sorte que PA = LU. Câblez des données à l'entrée A pour déterminer l'instance polymorphe à utiliser ou sélectionnez manuellement l'instance.

Entrées/Sorties
 A
—
A
—
A est une matrice réelle.  L
—
L
—
L est une matrice triangulaire inférieure avec des uns en diagonale.  U
—
U
—
U est une matrice triangulaire supérieure.  P
—
P
—
P est une matrice de permutation.  erreur
—
erreur
—
erreur renvoie toute erreur ou mise en garde générée par le VI. Vous pouvez câbler erreur au VI Convertir un code d'erreur en cluster d'erreur pour convertir le code d'erreur ou la mise en garde en cluster d'erreur. |
La factorisation LU VI factorise une matrice m × n A dans les types de matrices suivants, de sorte que PA = LU:
- L est une matrice m × min(m, n). Si m ≤ n, L est une matrice triangulaire inférieure avec des uns sur la diagonale. Si m > n, L est une matrice trapézoïdale inférieure avec des uns sur la diagonale.
- U est une matrice min(m, n) × n. Si m ≥ n, U est une matrice triangulaire supérieure. Si m < n, U est une matrice trapézoïdale supérieure.
- P est une matrice de permutation m × m, qui sert de matrice identité et dans laquelle certaines lignes ont été permutées.
Pour une matrice singulière, ce VI effectue une factorisation et renvoie une mise en garde, et il y a au moins un zéro sur la diagonale de U.
L'équation suivante illustre une propriété utile de la factorisation LU si A est une matrice carrée :
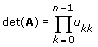
où det(A) est le déterminant de A.
La factorisation en LU constitue une étape cruciale dans l'inversion d'une matrice, le calcul du déterminant et la résolution d'une équation linéaire.
Exemples
Reportez-vous aux exemples de fichiers inclus avec LabVIEW suivants.
- labview\examples\Mathematics\Linear Algebra\Linear Algebra Calculator.vi