FFT
- Mise à jour2025-07-30
- Temps de lecture : 5 minute(s)
Calcule la transformée de Fourier rapide (FFT) de la séquence X en entrée. Câblez des données à l'entrée X pour déterminer l'instance polymorphe à utiliser ou sélectionnez manuellement l'instance.

FFT 1D
Pour les signaux 1D, le VI FFT calcule la Transformée de Fourier Discrète (DFT) de la séquence en entrée avec un algorithme de Transformée de Fourier rapide. La DFT 1D est définie de la manière suivante :
 pour n = 0, 1, 2, …, N–1
pour n = 0, 1, 2, …, N–1où x correspond à la séquence en entrée, N correspond au nombre d'éléments de x, et Y correspond au résultat de la transformée.
La résolution de fréquence, ou l'écart en fréquence entre les composantes de Y, correspond à :

où fe correspond à la fréquence d'échantillonnage.
Le tableau suivant illustre les éléments type de FFT {X} pour différentes valeurs de décalage et de taille de la FFT, où Y correspond à FFT {X} et n correspond à la taille de la FFT :
| n est pair (k = n/2) | n est impair (k = (n-1)/2) | |||
|---|---|---|---|---|
| Maj | Élément de tableau | Fréquence correspondante | Élément de tableau | Fréquence correspondante |
FAUX (valeur par défaut) |
Y0 | Composante CC | Y0 | Composante CC |
FAUX (valeur par défaut) |
Y1 | Δf | Y1 | Δf |
FAUX (valeur par défaut) |
Y2 | 2Δf | Y2 | 2Δf |
FAUX (valeur par défaut) |
Y3 | 3Δf | Y3 | 3Δf |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
FAUX (valeur par défaut) |
Yk–2 | (k–2)Δf | Yk–2 | (k–2)Δf |
FAUX (valeur par défaut) |
Yk–1 | (k–1)Δf | Yk–1 | (k–1)Δf |
FAUX (valeur par défaut) |
Yk | Fréquence de Nyquist | Yk | kΔf |
FAUX (valeur par défaut) |
Yk+1 | –(k–1)Δf | Yk+1 | –kΔf |
FAUX (valeur par défaut) |
Yk+2 | –(k–2)Δf | Yk+2 | –(k–1)Δf |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
FAUX (valeur par défaut) |
Yn–3 | –3Δf | Yn–3 | –3Δf |
FAUX (valeur par défaut) |
Yn–2 | –2Δf | Yn–2 | –2Δf |
FAUX (valeur par défaut) |
Yn–1 | –Δf | Yn–1 | –Δf |
| n est pair (k = n/2) | n est impair (k = (n-1)/2) | |||
| Maj | Élément de tableau | Fréquence correspondante | Élément de tableau | Fréquence correspondante |
| VRAI | Y0 | –(Fréquence de Nyquist) | Y0 | –kΔf |
| VRAI | Y1 | –(k–1)Δf | Y1 | –(k–1)Δf |
| VRAI | Y2 | –(k–2)Δf | Y2 | –(k–2)Δf |
| VRAI | Y3 | –(k–3)Δf | Y3 | –(k–3)Δf |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| VRAI | Yk–2 | –2Δf | Yk–2 | –2Δf |
| VRAI | Yk–1 | –Δf | Yk–1 | –Δf |
| VRAI | Yk | Composante CC | Yk | Composante CC |
| VRAI | Yk+1 | Δf | Yk+1 | Δf |
| VRAI | Yk+2 | 2Δf | Yk+2 | 2Δf |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| VRAI | Yn–3 | (k–3)Δf | Yn–3 | (k–2)Δf |
| VRAI | Yn–2 | (k–2)Δf | Yn–2 | (k–1)Δf |
| VRAI | Yn–1 | (k–1)Δf | Yn–1 | kΔf |
FFT 2D
Pour les signaux 2D, le VI FFT calcule la transformée de Fourier Discrète (DFT) de la matrice en entrée. Ce VI effectue une FFT 1D sur les lignes de la matrice en entrée et effectue ensuite une FFT 1D sur les colonnes de la sortie de l'étape précédente. La DFT d'une matrice (M, N) est définie par :
 pour u = 0, 1, ..., M-1, v=0, 1, ..., N-1
pour u = 0, 1, ..., M-1, v=0, 1, ..., N-1où x correspond à la matrice en entrée et Y correspond au résultat de la transformée.
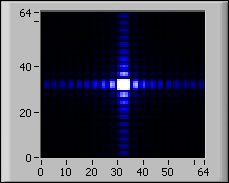
La figure suivante montre l'effet de décalage ? sur le résultat de la FFT 2D :
| signaux en entrée 2D | FFT sans décalage | FFT avec décalage |
|---|---|---|
 |
 |
 |
Exemples
Reportez-vous aux exemples de fichiers inclus avec LabVIEW suivants.
- labview\examples\Signal Processing\Transforms\FFT and Power Spectrum Units.vi