Matrice d'autocorrélation (DBL)
- Mise à jour2025-07-30
- Temps de lecture : 4 minute(s)
Calcule la matrice d'autocorrélation de la séquence X en entrée. Câblez des données à l'entrée X pour déterminer l'instance polymorphe à utiliser ou sélectionnez manuellement l'instance.

Entrées/Sorties
 initial ?
—
initial ?
—
initial ? contrôle l'initialisation du buffer interne. La valeur par défaut est FAUX. Lors de la première exécution de ce VI ou lorsque initial ? est VRAI, LabVIEW initialise le buffer interne à vide. Si initial ? est FAUX, LabVIEW initialise le buffer interne aux points de données finaux à partir de l'appel précédent de cette instance. Pour traiter une grande séquence de données composée de blocs plus petits, définissez cette entrée à VRAI pour le premier bloc et à FAUX pour le traitement continu de tous les autres blocs.  X
—
X
—
X est la séquence en entrée.  ordre
—
ordre
—
ordre spécifie l'ordre de la Matrice d'autocorrélation. Si l'ordre est inférieur à zéro, ce VI renvoie une erreur. La valeur par défaut est 0.  méthode
—
méthode
—
méthode spécifie la méthode utilisée pour calculer la matrice d'autocorrélation.
 Matrice d'autocorrélation
—
Matrice d'autocorrélation
—
Matrice d'autocorrélation renvoie la matrice d'autocorrélation de X de taille (ordre +1) multiplié par (ordre +1).  erreur
—
erreur
—
erreur renvoie toute erreur ou mise en garde générée par le VI. Vous pouvez câbler erreur au VI Convertir un code d'erreur en cluster d'erreur pour convertir le code d'erreur ou la mise en garde en cluster d'erreur. |
Ce VI utilise l'équation suivante pour calculer la matrice d'autocorrélation :

où M est la Matrice d'autocorrélation, R la matrice de données, et s un facteur de normalisation. RH est la transposée conjuguée de la matrice R.
Si la méthode est Autocorrélation, R est une matrice dont la taille est (N+k, k+1), définie comme suit.

où xi est l'i-ème élément de X, N correspond à la longueur deX et k à l'ordre. Le facteur de normalisation, s, est égal à N.
Si la méthode est Préfenêtrage, R est une matrice dont la taille est N sur (k+1) , définie comme suit.

Le facteur de normalisation, s, est égal à N.
Si la méthode est Postfenêtrage, R est une matrice dont la taille est N sur (k+1) , définie comme suit.

Le facteur de normalisation, s, est égal à N.
Si la méthode est Covariance, R est une matrice dont la taille est (N-k) sur (k+1), définie comme suit.

Le facteur de normalisation, s, est égal à N-k.
Si la méthode est Covariance modifiée, R est une matrice dont la taille est 2(N-k) sur (k+1), définie comme suit.

où xi* est la conjuguée complexe de xi. Le facteur de normalisation, s, est égal à 2*(N-k).
Ce VI supporte le mode mono-déclenchement et le mode continu. La figure suivante montre comment utiliser le VI Matrice d'autocorrélation en mode mono-déclenchement et en mode continu. Les deux sorties, Matrice d'autocorrélation 1 et Matrice d'autocorrélation 2, produisent toujours les mêmes résultats.
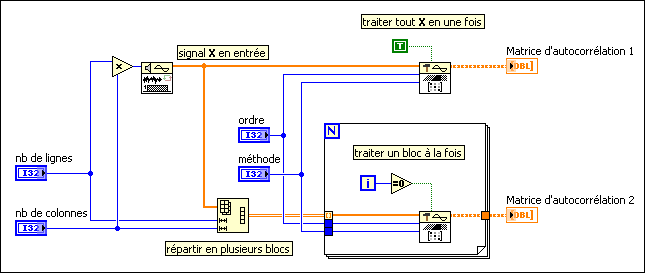
La matrice d'autocorrélation est largement utilisée dans le domaine de l'analyse spectrale pour estimer les composantes spectrales du signal d'entrée. En général, les méthodes Covariance et Covariance modifiée donnent de meilleurs résultats dans l'estimation spectrale que les méthodes Autocorrélation, Préfenêtrage et Postfenêtrage. National Instruments recommande d'utiliser la méthode de la covariance ou de la covariance modifiée pour estimer la matrice d'autocorrélation lors de l'analyse du spectre.