I/Q is a common way to represent message signals in modern communication systems.

As described in Modulation, there are two fundamental ways (degrees of freedom) to produce a modulated wave from a carrier wave. You can either perturb its amplitude or its phase. I/Q signaling allows you to simultaneously change both amplitude and phase. Using both degrees of freedom when modulating a carrier allows greater spectral efficiency with regard to bits per hertz of channel bandwidth (for a given bits per second transmission rate) than if using only one degree of freedom.

To simultaneously perturb both the amplitude and phase of a carrier, two canonical forms of frequency-translating transmitters simultaneously use the two degrees of freedom in modulation.

Canonical Polar Modulation

In polar modulation, the message signal is split into two components: R(t) controls the carrier wave amplitude changes, and φ(t) drives the carrier wave phase changes.

Canonical Rectangular Modulation

In rectangular modulation, the message signal is also split into two components: I(t) controls the in-phase carrier wave changes, and Q(t) controls the quadrature-phase carrier wave changes.

The Mathematical Relationship

The modulated outputs of the two canonical forms are mathematically and physically equivalent. To show their equality, you can compare and translate between the polar and rectangular representations.

Begin with the equation:

R ( t ) cos ( ω c ( t ) + φ ( t ) )

Plug in the following trigonometric identity:

cos ( α + β ) = cos ( α ) cos ( β ) − sin ( α ) sin ( β )

to yield the following equation:

R ( t ) [ cos ω c ( t ) cos φ ( t ) − sin ω c ( t ) sin φ ( t ) ]

When you simplify this equation, you have the following relationship:

I ( t ) cos ( ω c ( t ) ) − Q ( t ) sin ( ω c ( t ) )

where

  • I(t) = R(t) cos (φ(t))
  • Q(t) = R(t) sin (φ(t))
  • ωc = 2πfc
  • fc is the carrier frequency in Hertz

The rectangular form of modulation, often called I/Q Modulation, has become popular for certain technical reasons.

In the rectangular modulation figure, the real baseband signals of I(t) and Q(t) are created (in some way) to contain all the information of message input m(t). (The polar R(t) and φ(t) also contain the information of m(t).) Because the carriers cos(ωc(t)) and sin(ωc(t)) are orthogonal functions, we use the terminology of quadrature modulation

where

  • The signal applied to the cosine mixer is called the in-phase component (I)
  • The signal applied to the sine mixer is called the quadrature-phase component (Q)

The I and Q designations are useful because the I(t) baseband signal is applied to the cosine mixer, and the Q(t) baseband signal is applied to the sine mixer.

The analytical relationship between the polar form (R(t) and φ(t)) of the baseband signal and Cartesian form (I(t) and Q(t)) of the baseband signal is shown in the following figure.

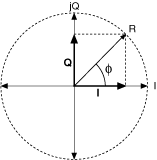
The diagram is a "snapshot in time" of the complex (analytical) baseband envelope g(t). Because the diagram is for an arbitrary instant in time, the independent time variable t is dropped. The amplitude of Q is projected onto the imaginary (j) axis and the amplitude of I is projected onto the real axis.

Note For a more thorough analysis of the complex mathematical relationship between the polar and rectangular forms, refer to Digital and Analog Communication Systems by Leon W. Couch.

I/Q modulation produces a single-sideband suppressed carrier waveform to modulate baseband signals. A lower sideband suppressed carrier can be configured with the following equations:

R F 1 = sin ω c t · A sin ω b t = A 2 cos ω c - ω b t - A 2 cos ω c + ω b t
R F 2 = cos ω b t · A cos ω b t = A 2 cos ω c - ω b t + A 2 cos ω c - ω b t

where

  • ωc represents the carrier frequency
  • ωb represents the baseband frequency
  • t represents time