Konvertiert eine (3,3)-Matrix von Richtungscosinuswerten in eulersche Winkel.


icon

Ein-/Ausgänge

  • c2ddbl.png Richtungscosinus —

    Richtungscosinus gibt die (3,3)-Matrix aus Richtungscosinuswerten an, mit der die Punkte des alten Koordinatenrahmens auf den neuen umgerechnet werden. Jedes Element der Matrix muss im Bereich von –1 bis 1 liegen.

  • cu16.png Drehreihenfolge —

    Drehreihenfolge gibt die Reihenfolge der Achsen an, um die die Koordinaten gedreht werden sollen.

    Beispielsweise wird mit X-Y-Z angegeben, dass die erste Drehung um die x-Achse stattfinden soll, die zweite um die y-Achse und die dritte um die z-Achse. Die Standardreihenfolge lautet Z-X-Z.

    0X-Y-Z
    1X-Z-Y
    2Y-X-Z
    3Y-Z-X
    4Z-X-Y
    5Z-Y-X
    6X-Y-X
    7X-Z-X
    8Y-X-Y
    9Y-Z-Y
    10Z-X-Z
    11Z-Y-Z
  • inclst.png Euler-Winkel —

    Euler-Winkel gibt die eulerschen Winkel im Bogenmaß aus.

  • idbl.png Phi —

    Phi gibt den Drehwinkel um die erste Achse im Bogenmaß aus.

  • idbl.png Theta —

    Theta gibt den Drehwinkel um die zweite Achse im Bogenmaß aus.

  • idbl.png Psi —

    Psi gibt den Drehwinkel um die dritte Achse im Bogenmaß aus.

  • ii32.png Fehler —

    Fehler gibt alle Fehler oder Warnungen des VIs aus. Zur Umwandlung eines Fehlercodes oder einer Warnung in einen Fehler-Cluster verbinden Sie Fehler mit dem VI Fehler-Cluster aus Fehlercode.

    • Eine Rotation kann entweder mit dem Richtungscosinus oder dem Euler-Winkel durchgeführt werden. Die Beziehung zwischen Richtungscosinus und Euler-Winkel lautet bei der Standarddrehreihenfolge Z-X-Z folgendermaßen:

    R =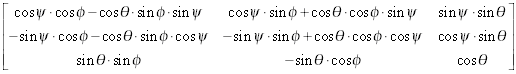

    wobei R die eingegebene 3-mal-3-Richtungs-Kosinus-Matrix ist. ϕ (-π < ϕ ≤ π), θ (0 ≤ θ ≤ π) und ψ (-π < ψ ≤ π) sind die ausgegebenen Euler-Winkel im Bogenmaß.