Berechnet die Kreuzkorrelation der Eingangsfolgen X und Y. Zur Bestimmung der Instanz des polymorphen VIs verbinden Sie Daten mit den Eingängen X und Y oder wählen Sie die Instanz manuell aus.


icon

1D-Kreuzkorrelation

Die Kreuzkorrelation Rxy(t) der Folgen x(t) und y(t) ist durch folgende Gleichung definiert:

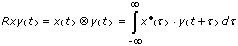
wobei das Symbol ⊗ für die Korrelation steht.

Die diskrete Implementierung dieses VIs erfolgt wie nachfolgend beschrieben. Gegeben sei h als eine Folge, deren Indizierung negativ sein kann, N sei die Anzahl der Elemente der Eingangsfolge X, M die Anzahl der Elemente der Folge Y. Es wird angenommen, dass die indizierten Elemente von X und Y außerhalb des Bereichs 0 sind.

xj = 0, j < 0 oder j ≥ N

und

yj = 0, j < 0 oder j ≥ M.

Die Elemente von h werden nach folgender Gleichung bestimmt:

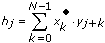
für j = –(N–1), –(N–2), … , –1, 0, 1, … , (M–2), (M–1)

Die Elemente der Ausgangsfolge Rxy stehen mit den Elementen in der Folge h in folgender Relation:

Rxyi = hi – (N–1)

für i = 0, 1, 2, … , N+M–2.

Da LabVIEW-Arrays keine negativen Indizes haben dürfen, ist der entsprechende Kreuzkorrelationswert für t = 0 das N-te Element der Ausgangsfolge Rxy. Daher stellt Rxy die Korrelationswerte dar, die bei der Indizierung N Mal verschoben werden.

Das folgende Blockdiagramm zeigt eine Möglichkeit zur Indizierung des VIs:

Der folgende Graph ist das Ergebnis des vorherigen Blockdiagramms:

Zur Verbesserung der Rechengenauigkeit müssen die Werte in einigen Fällen normiert werden. Mit diesem VI ist eine verzerrte und unverzerrte Normalisierung möglich.

  1. Verzerrte Normalisierung

    Wenn die Normalisierung verzerrtist, wendet LabVIEW die verzerrte Normalisierung wie folgt an:

    Rxy(verzerrt)j =

    für j = 0, 1, 2, ... ,M+N-2

    wobei Rxy die Kreuzkorrelation von x und y ohne Normierung ist.

  2. Unverzerrte Normalisierung

    Wenn die Normierung unverzerrtist, wendet LabVIEW die unverzerrte Normierung wie folgt an:

    Rxy(unverzerrt)j =

    für j = 0, 1, 2, ... ,M+N-2

    wobei Rxy die Kreuzkorrelation zwischen x und y ohne Normierung ist. f(j) ist:

2D-Kreuzkorrelation

Mit dem VI "Kreuzkorrelation" wird die zweidimensionale Kreuzkorrelation berechnet:

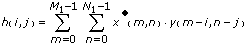
für i = –(M1–1), … , –1, 0, 1, … , (M2–1) and j = –(N1–1), … , –1, 0, 1, … , (N2–1)

wobei M1 die Zeilenanzahl der Matrix X,

N1 ist die Anzahl der Spalten der Matrix X, M2 ist die Anzahl der Zeilen der Matrix Y, N2 ist die Anzahl der Spalten der Matrix Y, die indizierten Elemente außerhalb der Bereiche von X und Y sind gleich Null, wie in den folgenden Beziehungen gezeigt:

x(m,n) = 0, m < 0 oder m ≥ M1 oder n < 0 oder n ≥ N1

und

y(m,n) = 0, m < 0 oder m ≥ M2 oder n < 0 oder n ≥ N2.

Die Elemente der Ausgangsmatrix Rxy stehen mit den Elementen von h in folgender Relation:

Rxy(l,j) = h(i–[M1–1], j–[N1–1]) für i = 0, 1, 2, … , M1+M2–2 und j = 0, 1, 2, … , N1+N2–2.