Berechnet die Kreuzkorrelation der Eingangsfolgen X und Y. Zur Auswahl der polymorphen Instanz verbinden Sie Daten mit dem Eingang X oder Y oder wählen Sie die Instanz manuell aus.


icon

Ein-/Ausgänge

  • c1ddbl.png X —

    X ist die erste Eingangsfolge.

  • c1ddbl.png Y —

    Y ist die zweite Eingangsfolge.

  • cenum.png Algorithmus —

    Algorithmus gibt die zu verwendende Korrelationsmethode an. Wenn Algorithmus auf direct eingestellt ist, wird die Kreuzkorrelation anhand des direkten Verfahrens der linearen Korrelation berechnet. Bei frequency domain berechnet das VI die Kreuzkorrelation nach einem Verfahren, das auf der FFT beruht.

    Wenn X und Y klein sind, ist die Methode direct in der Regel schneller. Wenn X und Y groß sind, ist die Methode frequency domain in der Regel schneller. Daneben kann es zwischen den zwei Verfahren geringe Abweichungen geben.

    0
    direct
    1
    frequency domain
    (Voreinstellung)
  • cenum.png Normalisierung —

    Normalisierung gibt das Normalisierungsverfahren zur Berechnung der Kreuzkorrelation zwischen X und Y an.

    0
    none
    (Voreinstellung)
    1
    unbiased
    2
    biased
  • i1ddbl.png Rxy —

    Rxy ist die Kreuzkorrelation von X und Y.

  • ii32.png Fehler —

    Fehler gibt alle Fehler oder Warnungen des VIs aus. Zur Umwandlung eines Fehlercodes oder einer Warnung in einen Fehler-Cluster verbinden Sie Fehler mit dem VI Fehler-Cluster aus Fehlercode.

    • 1D-Kreuzkorrelation

    Die Kreuzkorrelation Rxy(t) der Folgen x(t) und y(t) ist durch folgende Gleichung definiert:

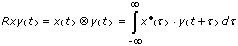
    wobei das Symbol ⊗ für die Korrelation steht.

    Die diskrete Implementierung dieses VIs erfolgt wie nachfolgend beschrieben. Gegeben sei h als eine Folge, deren Indizierung negativ sein kann, N sei die Anzahl der Elemente der Eingangsfolge X, M die Anzahl der Elemente der Folge Y. Es wird angenommen, dass die indizierten Elemente von X und Y außerhalb des Bereichs 0 sind.

    xj = 0, j < 0 oder j ≥ N

    und

    yj = 0, j < 0 oder j ≥ M.

    Die Elemente von h werden nach folgender Gleichung bestimmt:

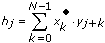
    für j = –(N–1), –(N–2), … , –1, 0, 1, … , (M–2), (M–1)

    Die Elemente der Ausgangsfolge Rxy stehen mit den Elementen in der Folge h in folgender Relation:

    Rxyi = hi – (N–1)

    für i = 0, 1, 2, … , N+M–2.

    Da LabVIEW-Arrays keine negativen Indizes haben dürfen, ist der entsprechende Kreuzkorrelationswert für t = 0 das N-te Element der Ausgangsfolge Rxy. Daher stellt Rxy die Korrelationswerte dar, die bei der Indizierung N Mal verschoben werden.

    Das folgende Blockdiagramm zeigt eine Möglichkeit zur Indizierung des VIs:

    Der folgende Graph ist das Ergebnis des vorherigen Blockdiagramms:

    Zur Verbesserung der Rechengenauigkeit müssen die Werte in einigen Fällen normiert werden. Mit diesem VI ist eine verzerrte und unverzerrte Normalisierung möglich.

    1. Verzerrte Normalisierung

      Wenn die Normalisierung verzerrtist, wendet LabVIEW die verzerrte Normalisierung wie folgt an:

      Rxy(verzerrt)j =

      für j = 0, 1, 2, ... ,M+N-2

      wobei Rxy die Kreuzkorrelation von x und y ohne Normierung ist.

    2. Unverzerrte Normalisierung

      Wenn die Normierung unverzerrtist, wendet LabVIEW die unverzerrte Normierung wie folgt an:

      Rxy(unverzerrt)j =

      für j = 0, 1, 2, ... ,M+N-2

      wobei Rxy die Kreuzkorrelation zwischen x und y ohne Normierung ist. f(j) ist: