通过Levenberg-Marquardt算法获得的参数集合，该集合是输入数据点(X, Y)的最佳拟合，数据点可由非线性函数y＝f(x,a)表示，a是参数的集合。必须手动选择所需多态实例。


icon

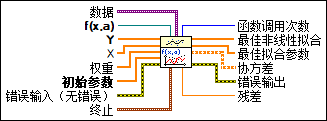
输入/输出

  • cfxdt.png 数据 —

    数据指定用户定义函数运行时所需的静态数据。

  • csvrn.png f(x,a) —

    f(x,a)是VI引用，用于实现拟合模型。a是LabVIEW计算的一组参数。

    使用位于 labview\vi.lib\gmath\NumericalOptimization\LM模型函数和gradient.vit的 VI模板， ，从模板创建VI。

  • c1ddbl.png Y —

    Y指定因变量数组或观测值。输入点的数量必须大于等于0。

  • c1ddbl.png X —

    X指定自变量数组。输入点的数量必须大于等于0。

  • c1ddbl.png 权重 —

    权重是观测点Y的权重数组。如权重未连线，VI将把权重的所有元素设置为1。

    如权重的元素数小于Y，VI将用1填充权重，使权重的长度等于Y。如权重的元素数大于Y，VI将忽略权重中多余的元素。如权重中的某个元素小于0，VI将使用元素的绝对值。

  • c1ddbl.png 初始参数 —

    初始参数指定最佳拟合参数的初始猜测。初始参数的长度必须等于f(x,a)中a的长度。

    非线性曲线拟合是否成功取决于初始参数与最佳拟合参数的接近程度。所以，使用该VI前应使用一切可能的资源，得到该参数的最佳初始猜测。

  • cerrcodeclst.png 错误输入（无错误） —

    错误输入表明该节点运行前发生的错误条件。该输入提供标准错误输入功能。

  • cnclst.png 终止 —

    终止指定拟合过程的终止条件。

  • ci32.png 最大循环次数 —

    最大循环次数指定拟合的最大循环次数。如循环次数超过最大循环次数，拟合过程将停止。

  • cdbl.png 容忍度 —

    容差指定Y和当前拟合间加权距离的相对变化。如相对变化低于容差，拟合过程将停止。

  • ii32.png 函数调用次数 —

    函数调用次数返回拟合过程中LabVIEW调用f(x,a)的次数。

  • i1ddbl.png 最佳非线性拟合 —

    最佳线性拟合返回对应于X中独立变量的拟合模型的y值。

  • i1ddbl.png 最佳拟合参数 —

    最佳拟合参数返回的参数数组可将最佳非线性拟合和观测的Y值之间的加权均方误差降至最低。

  • i2ddbl.png 协方差 —

    协方差返回协方差矩阵。

    Cjk是a[j]和a[k]之间的协方差。c[jj]是a[j]的方差。这个VI产生 协方差， C，根据以下公式： C = (0.5D)^-1 其中 D 是函数关于其参数的Hessian。

  • ierrcodeclst.png 错误输出 —

    错误输出包含错误信息。该输出提供标准错误输出功能。

  • idbl.png 残差 —

    残差返回最佳非线性你和和Y值之间的加权均方误差。

    • 该VI通过Levenberg-Marquardt方法计算最佳拟合参数，以最小化Y的观测值与最佳非线性拟合之间的加权均方误差。下列方程为曲线模型：

    y[i] = f(x[i], a0, a1, a2, …)

    a0, a1, a2, …是参数。

    Levenberg-Marquardt方法无需y与参数之间存在线性关系。

    Hessian矩阵是数值优化方法（例如，牛顿方法）中常见的矩阵。为避免奇异Hessian矩阵的弱点，Levenberg-Marquardt方法为Hessian矩阵添加正定对角矩阵。该矩阵是Levenberg-Marquardt方法和牛顿方法的不同之处。关于Levenberg-Marquardt方法的更多信息，见数学相关文档中的数值优化。

    可使用非线性Levenberg-Marquardt法拟合线性和非线性曲线。拟合曲线时，广义线性拟合VI的效率更高。必须验证使用Levenberg-Marquardt方法获得的结果，该方法不保证一定能获得正确的结果。

    范例

    请参考LabVIEW附带的下列范例文件。

    • labview\examples\Mathematics\Fitting\Ellipse fit.vi
    • labview\examples\Mathematics\Fitting\Sum of 3 Gaussians with offset fit.vi
    • labview\examples\Mathematics\Fitting\Gaussian surface with offset fit.vi