使用欧拉角方法将三维直角坐标系按逆时针方向旋转，并返回给定点的新坐标。通过连线数据至X输入端可确定要使用的多态实例，也可手动选择实例。


icon

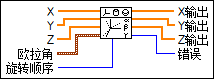
输入/输出

  • c1ddbl.png X —

    X指定输入的x坐标。

  • c1ddbl.png Y —

    Y指定输入的y坐标。

  • c1ddbl.png Z —

    Z指定输入的z坐标。

  • cnclst.png 欧拉角 —

    欧拉角指定欧拉角，以弧度为单位。

  • cdbl.png phi —

    phi指定第一个轴旋转的角度，以弧度为单位。

  • cdbl.png theta —

    theta指定第二个轴旋转的角度，以弧度为单位。

  • cdbl.png psi —

    psi指定第三个轴旋转的角度，以弧度为单位。

  • cu16.png 旋转顺序 —

    旋转顺序指定了旋转坐标的坐标轴的次序。

    例如，X-Y-Z表示第一个、第二个和第三个旋转分别为x轴、y轴和z轴。Z-X-Z是默认次序。

    0X-Y-Z
    1X-Z-Y
    2Y-X-Z
    3Y-Z-X
    4Z-X-Y
    5Z-Y-X
    6X-Y-X
    7X-Z-X
    8Y-X-Y
    9Y-Z-Y
    10Z-X-Z
    11Z-Y-Z
  • i1ddbl.png X输出 —

    X输出返回旋转后的x坐标。

  • i1ddbl.png Y输出 —

    Y输出返回旋转后的y坐标。

  • i1ddbl.png Z输出 —

    Z输出返回旋转后的z坐标。

  • ii32.png 错误 —

    错误返回VI的任何错误或警告。将错误连接至错误代码至错误簇转换VI，可将错误代码或警告转换为错误簇。

    • 根据欧拉旋转理论，你可以用欧拉角j、θ和ψ来描述一个坐标旋转，如下图所示（以默认旋转顺序 Z-X-Z 为例）：

    旋转可描述为下列三个步骤：

    1. 将X轴、Y轴和Z轴绕Z轴旋转j（-π<j≤π），得到X'、Y'和Z轴。
    2. 将X'-、Y'-和Z轴围绕X'-轴旋转θ（0≤θ≤π），得到X'-、Y''-和Z'-轴。
    3. 将X''、Y''和Z''轴围绕Z''轴旋转ψ（-π < ψ ≤ π），得到X''、Y'''和Z''轴的结果。

    如通过下列三个矩阵B, C和D表述点(x, y, z)的旋转：

    ; ; ,

    在新坐标系中，点的坐标(x', y', z')为

    A = BCD。