FFT
- 更新时间2025-07-30
- 阅读时长5分钟
计算输入序列X的快速傅立叶变换(FFT)。通过连线数据至X输入端可确定要使用的多态实例,也可手动选择实例。

一维FFT
对于一维信号,该VI使用快速傅立叶变换算法计算输入序列的离散傅立叶变换(DFT)。一维DFT定义如下:
 n = 0, 1, 2, …, N–1
n = 0, 1, 2, …, N–1x是输入序列,N是x中元素的数量,Y是变换的结果。
Y成分的频域分辨率(频率间隔)为:
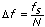
fs是采样频率。
下表为不同FFT大小和移位值的FFT {X}的元素模式,Y是FFT {X},n是FFT大小:
| n为偶数(k = n/2) | n为奇数(k = (n-1)/2) | |||
|---|---|---|---|---|
| Shift | 数组元素 | 相关频率 | 数组元素 | 相关频率 |
FALSE (默认) |
Y0 | 直流分量 | Y0 | 直流分量 |
FALSE (默认) |
Y1 | Δf | Y1 | Δf |
FALSE (默认) |
Y2 | 2Δf | Y2 | 2Δf |
FALSE (默认) |
Y3 | 3Δf | Y3 | 3Δf |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
FALSE (默认) |
Yk–2 | (k-2)Δf | Yk–2 | (k-2)Δf |
FALSE (默认) |
Yk–1 | (k-1)Δf | Yk–1 | (k-1)Δf |
FALSE (默认) |
Yk | 奈奎斯特频率 | Yk | kΔf |
FALSE (默认) |
Yk+1 | -(k-1)Δf | Yk+1 | -kΔf |
FALSE (默认) |
Yk+2 | -(k-2)Δf | Yk+2 | -(k-1)Δf |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
FALSE (默认) |
Yn–3 | -3Δf | Yn–3 | -3Δf |
FALSE (默认) |
Yn–2 | -2Δf | Yn–2 | -2Δf |
FALSE (默认) |
Yn–1 | -Δf | Yn–1 | -Δf |
| n为偶数(k = n/2) | n为奇数(k = (n-1)/2) | |||
| Shift | 数组元素 | 相关频率 | 数组元素 | 相关频率 |
| TRUE | Y0 | -(奈奎斯特频率) | Y0 | -kΔf |
| TRUE | Y1 | -(k-1)Δf | Y1 | -(k-1)Δf |
| TRUE | Y2 | -(k-2)Δf | Y2 | -(k-2)Δf |
| TRUE | Y3 | -(k-3)Δf | Y3 | -(k-3)Δf |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| TRUE | Yk–2 | -2Δf | Yk–2 | -2Δf |
| TRUE | Yk–1 | -Δf | Yk–1 | -Δf |
| TRUE | Yk | 直流分量 | Yk | 直流分量 |
| TRUE | Yk+1 | Δf | Yk+1 | Δf |
| TRUE | Yk+2 | 2Δf | Yk+2 | 2Δf |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| TRUE | Yn–3 | (k-3)Δf | Yn–3 | (k-2)Δf |
| TRUE | Yn–2 | (k-2)Δf | Yn–2 | (k-1)Δf |
| TRUE | Yn–1 | (k-1)Δf | Yn–1 | kΔf |
二维FFT
对于二维信号,该VI计算输入矩阵的离散傅立叶变换(DFT)。该VI对输入矩阵的行进行一维FFT,然后在上一步输出的列上进行一维FFT。M×N矩阵的DFT定义如下:
 对于 u =0,1,..., M-1, v=0,1,..., N-1
对于 u =0,1,..., M-1, v=0,1,..., N-1x是输入矩阵,Y是变换的结果。
下图为移位?对二维FFT结果的影响:
| 二维输入信号 | 无移位的FFT | 有移位的FFT |
|---|---|---|
 |
 |
 |
范例
请参考LabVIEW附带的下列范例文件。
- labview\examples\Signal Processing\Transforms\FFT and Power Spectrum Units.vi