计算输入序列X和Y的卷积。通过连线数据至x和y输入端可确定要使用的多态实例，也可手动选择实例。


icon

输入/输出

  • c2ddbl.png X —

    X是第一个输入序列。

  • c2ddbl.png Y —

    Y是第二个输入序列。

  • cenum.png 算法 —

    算法指定使用的卷积方法。算法的值为direct时，VI使用线性卷积的direct方法计算卷积。算法为frequency domain时，VI使用基于FFT的方法计算卷积。

    如果 X 和 Y 较小， direct 方法通常更快。如果 X 和 Y 较大， frequency domain 方法通常更快。此外，两个方法数值上存在微小的差异。

    0
    direct
    1
    frequency domain
    （默认）
  • cenum.png 输出大小 —

    输出大小确定X*Y的大小。

    0full (默认）-将 X * Y 的宽度设置为小于 X 和 Y 的宽度之和，将 X * Y 的高度设置为小于 X 和 Y的高度之和。
    1size X-将 X * Y 的宽度和高度设置为 X的宽度和高度。
    2compact-将 X * Y 的宽度设置为大于 X 和 Y 宽度之差的数值，将 X * Y 的高度设置为大于 X 和 Y高度之差的数值。输出大小为compact时，X的宽度和高度必须分别大于或等于Y的宽度和高度。
  • i2ddbl.png X * Y —

    X * Y是X和Y的卷积。

  • ii32.png 错误 —

    错误返回VI的任何错误或警告。将错误连接至错误代码至错误簇转换VI，可将错误代码或警告转换为错误簇。

    • 二维卷积

    算法为direct时，该VI使用下列方程计算输入矩阵X和Y的二维卷积。

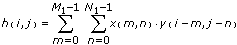
    i = 0, 1, 2, …，M1+M2–2，j = 0, 1, 2, … , N1+N2–2

    h为X * Y，

    M1 是矩阵 X的行数、 N1 是矩阵 X的列数、 M2 是矩阵 Y的行数、 N2 是矩阵 Y的列数、 在 X 和 Y 的范围之外的索引元素等于零，如以下关系所示：

    x(m,n), m < 0 或 m ≥M1 或 n < 0 或 n ≥N1

    且

    y(m,n) , m < 0 或 m ≥M2 或 n < 0 或 n ≥N2。

    如算法为frequency domain，VI按照下列步骤计算二维卷积：

    • 首先，该VI用0填充X和Y的末尾，使信号的大小满足(M1 + M2 – 1)行(N1 + N2 – 2)列。如下列方程所示。
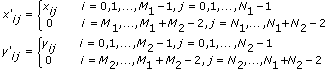
    • 然后，VI按照下列公式对X'和Y'进行傅立叶变换。
    X'(f) = FFT(x') Y'(f) = FFT(y')
    • 最后，VI将X'(f)乘以Y'(f)，并计算乘积的反傅立叶变换。结果为X和Y的二维卷积，如下列等式所示：
    X * Y = IFFT(X'(f) · Y'(f))

    输出大小可确定输出矩阵X * Y的大小。如下图所示。

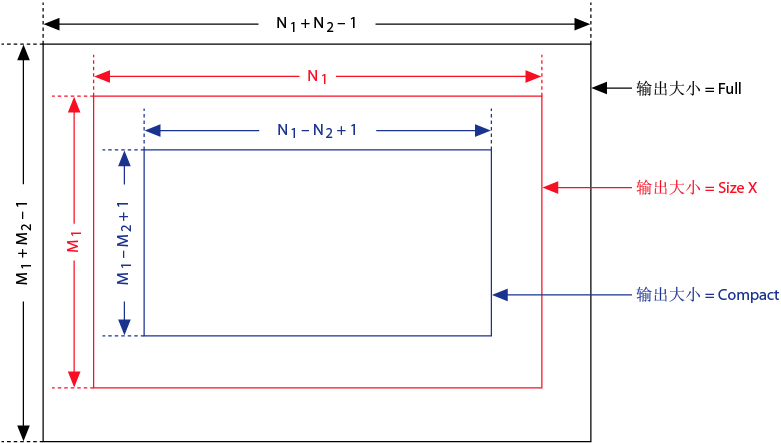
    1. full

      输出矩阵X * Y为(M1+M2–1)行(N1+N2–1)列。

    2. size X

      适用于图像处理。如X是要滤波的图像，Y为小矩阵，称为卷积核。X * Y是滤波后的图像，大小和图像X相同。输出大小为full时，M1*N1输出矩阵是输出矩阵的中心部分。

    3. compact

      如输出大小为full或size X，计算X * Y的边缘元素要求零填充。如输出大小为compact，LabVIEW将删除此类边缘元素。如输出大小为size X，(M1–M2+1)*(N1–N2+1)输出矩阵是输出矩阵的中心部分。

    范例

    请参考LabVIEW附带的下列范例文件。

    • labview\examples\Signal Processing\Signal Operation\Edge Detection with 2D Convolution.vi