입력 시퀀스 X의 빠른 푸리에 변환(FFT)을 계산합니다. 데이터를 X 입력에 연결하여 사용할 다형성 인스턴스를 결정하거나 인스턴스를 수동으로 선택합니다.


icon

1D FFT

1D 신호에서 FFT VI는 빠른 푸리에 변환 알고리즘으로 입력 시퀀스의 Discrete Fourier Transform (DFT)을 계산합니다. 1D DFT는 다음과 같이 정의됩니다:

여기서 n=0, 1, 2,…, N-1

이 때 x는 입력 시퀀스, N은 x의 원소 개수, Y는 변환 결과입니다.

주파수 분해능, 또는 Y 성분 사이의 주파수 공간은 다음과 같습니다:

이 때 fs는 샘플링 주파수입니다.

다음 테이블은 Y가 FFT {X}이고 n이 FFT 크기일 때 다양한 FFT 크기와 이동 값을 위한 FFT {X}의 원소 패턴을 나타냅니다.

n은 짝수 (k = n/2)n은 홀수 (k = (n-1)/2)
<Shift> 배열 원소 대응하는 주파수 배열 원소 대응하는 주파수

거짓

(기본)

 Y0 DC 성분 Y0 DC 성분

거짓

(기본)

 Y1 Δf Y1 Δf

거짓

(기본)

 Y2 2Δf Y2 2Δf

거짓

(기본)

 Y3 3Δf Y3 3Δf
⋮ ⋮ ⋮ ⋮ ⋮

거짓

(기본)

 Yk–2 (k-2)Δf Yk–2 (k-2)Δf

거짓

(기본)

 Yk–1 (k-1)Δf Yk–1 (k-1)Δf

거짓

(기본)

 Yk 나이퀴스트 주파수 Yk kΔf

거짓

(기본)

 Yk+1 -(k-1)Δf Yk+1 -kΔf

거짓

(기본)

 Yk+2 -(k-2)Δf Yk+2 -(k-1)Δf
⋮ ⋮ ⋮ ⋮ ⋮

거짓

(기본)

 Yn–3 -3Δf Yn–3 -3Δf

거짓

(기본)

 Yn–2 -2Δf Yn–2 -2Δf

거짓

(기본)

 Yn–1 -Δf Yn–1 -Δf
n은 짝수 (k = n/2)n은 홀수 (k = (n-1)/2)
<Shift> 배열 원소 대응하는 주파수 배열 원소 대응하는 주파수
참 Y0 –(나이퀴스트 주파수) Y0 -kΔf
참 Y1 -(k-1)Δf Y1 -(k-1)Δf
참 Y2 -(k-2)Δf Y2 -(k-2)Δf
참 Y3 -(k-3)Δf Y3 -(k-3)Δf
⋮ ⋮ ⋮ ⋮ ⋮
참 Yk–2 -2Δf Yk–2 -2Δf
참 Yk–1 -Δf Yk–1 -Δf
참 Yk DC 성분 Yk DC 성분
참 Yk+1 Δf Yk+1 Δf
참 Yk+2 2Δf Yk+2 2Δf
⋮ ⋮ ⋮ ⋮ ⋮
참 Yn–3 (k-3)Δf Yn–3 (k-2)Δf
참 Yn–2 (k-2)Δf Yn–2 (k-1)Δf
참 Yn–1 (k-1)Δf Yn–1 kΔf

2D FFT

2D 신호에서 FFT VI는 입력 행렬의 Discrete Fourier Transform (DFT)을 계산합니다. 이 VI는 입력 행렬의 행에 1D FFT를 수행한 다음에 이전 단계 출력의 열에 1D FFT를 수행합니다. M xN 행렬의 DFT는 다음과 같이 정의됩니다:

u = 0, 1, ..., M-1, v=0, 1, ..., N-1의경우

이 때 x는 입력 행렬이고 Y는 변환 결과입니다.

아래 그림은 2D FFT 결과에서 이동?의 효과를 보여줍니다:

2D 입력 신호 이동없는 FFT 이동있는 FFT

관련 정보

FFT 기반의 VI에 대한 출력 단위

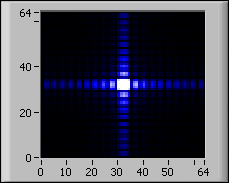예제

LabVIEW 포함되는 다음 예제 파일을 참조하십시오.

  • labview\examples\Signal Processing\Transforms\FFT and Power Spectrum Units.vi