Fonction Gamma incomplète complémentaire
- Mise à jour2025-07-30
- Temps de lecture : 2 minute(s)
Calcule la fonction gamma incomplète complémentaire régularisée.

Entrées/Sorties
 x
—
x
—
x est l'argument en entrée. Si x est négatif, le VI utilise la valeur absolue de x.  a
—
a
—
a est la limite inférieure de l'intégrale gamma incomplète complémentaire régularisée.  1 - g(x, a)
—
1 - g(x, a)
—
1 - g(x, a) renvoie la valeur de la fonction gamma incomplète complémentaire régularisée. |
L'équation suivante définit le complément de la fonction gamma incomplète régularisée.
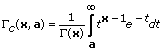
Le complément de la fonction gamma incomplète régularisée est lié à la fonction gamma incomplète régularisée par l'identité suivante.

La fonction gamma incomplète régularisée est définie pour les valeurs en entrée situées dans les intervalles suivants.

Pour toute valeur réelle positive de la limite inférieure a, la fonction gamma incomplète régularisée est définie pour les valeurs réelles non négatives de x.