Résout un système linéaire, de n dimension, d'équations différentielles avec une condition initiale donnée. La solution est basée sur la détermination des valeurs propres et des vecteurs propres de la matrice sous-jacente. La solution est donnée sous forme symbolique.


icon

Entrées/Sorties

  • c2ddbl.png A (matrice de coefficients) —

    A est la matrice (n, n) décrivant le système linéaire.

  • c1ddbl.png X0 (valeur de départ) —

    X0 est le vecteur n décrivant la condition initiale x[10], …, x[n0].

    Il existe une correspondance bijective entre les composantes de X0 et celles de X.

  • istr.png formule —

    formule est une chaîne contenant la solution du système linéaire dans la notation de formule standard de LabVIEW. Les éléments du vecteur solution sont séparés par un retour chariot.

  • ii32.png erreur —

    erreur renvoie toute erreur ou mise en garde générée par le VI. Des erreurs se produisent lors de l'utilisation d'entrées X, X0 et F(X,t) incorrectes. Vous pouvez câbler erreur au VI Convertir un code d'erreur en cluster d'erreur pour convertir le code d'erreur ou la mise en garde en cluster d'erreur.

    • Remarque Ce VI fonctionne bien pour la plupart des matrices réelles A qui ont des valeurs propres répétées, des valeurs propres conjuguées complexes, et ainsi de suite. L'exception est le cas d'une matrice de vecteur propre singulière, c'est-à-dire une matrice dans laquelle les vecteurs propres n'ont pas une portée couvrant la totalité de l'espace. Une erreur de -23016 est donnée si la matrice des vecteurs propres est singulière.

    L'équation différentielle linéaire décrite par le système suivant :

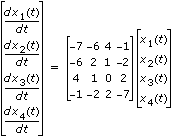
    avec

    x1(0) = 1 x2(0) = 2 x3(0) = 3 x4(0) = 4

    a pour solution

    + 1,62*e(-12,46*t) - 1,28*e(-6,30*t) + 0,63*e(1,34*t) + 0,04*e(5,42*t) + 0,84*e(-12,46*t) - 0,29*e(-6,30*t) + 1,51*e(1,34*t) - 0,06*e(5,42*t) -0,73*e(-12,46*t) + 0,01*e(-6,30*t) + 3,69*e(1,34*t) + 0,02*e(5,42*t) + 0,87*e(-12,46*t) + 2,67*e(-6,30*t) + 0,45*e(1,34*t) + 0,01*e(5,42*t)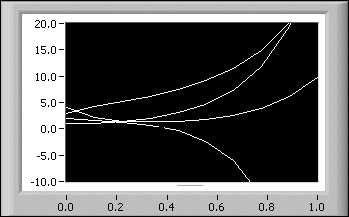

    La liste de paramètres suivante indique comment entrer les équations précédentes sur la face-avant :

    • A : [-7, -6, 4, 1; -6, 2, 1, -2; 4, 1, 0, 2; -1, -2, 2, -7]
    • X0 : [1, 2, 3, 4]