Résout un système linéaire homogène d'équations différentielles à coefficients constants, de n dimension, pour une condition initiale donnée.


icon

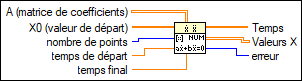
Entrées/Sorties

  • c2ddbl.png A (matrice de coefficients) —

    A est la matrice (n, n) décrivant le système linéaire.

  • c1ddbl.png X0 (valeur de départ) —

    X0 est le vecteur n décrivant la condition initiale x[10], …, x[n0].

    Il existe une correspondance bijective entre les composantes de X0 et celles de X.

  • cu32.png nombre de points —

    nombre de points est le nombre d'instants équidistants entre le temps de départ et la temps final. La valeur par défaut est 10.

  • cdbl.png temps de départ —

    temps de départ est le point de départ de l'ÉDO. La valeur par défaut est 0.

  • cdbl.png temps final —

    temps final est le point final de l'intervalle de temps étudié. La valeur par défaut est 1,0.

  • i1ddbl.png Temps —

    Temps est un tableau représentant les incréments de temps. La méthode utilise des incréments de temps équidistants entre le temps de départ et la temps final.

  • i2ddbl.png Valeurs X —

    Valeurs X est la matrice de la solution X aux instants équidistants.

  • ii32.png erreur —

    erreur renvoie toute erreur ou mise en garde générée par le VI. Des erreurs se produisent lors de l'utilisation d'entrées X, X0 et F(X,t) incorrectes. Vous pouvez câbler erreur au VI Convertir un code d'erreur en cluster d'erreur pour convertir le code d'erreur ou la mise en garde en cluster d'erreur.

    • La solution de ce VI est basée sur la détermination des valeurs propres et des vecteurs propres de la matrice A sous-jacente. La solution est donnée sous forme numérique.

    Remarque Ce VI fonctionne bien pour la plupart des matrices réelles A qui ont des valeurs propres répétées, des valeurs propres conjuguées complexes, et ainsi de suite. L'exception est le cas d'une matrice de vecteurs propres singulières, c'est-à-dire une matrice dans laquelle les vecteurs propres n'ont pas une portée couvrant la totalité de l'espace. Une erreur de -23016 est donnée si la matrice des vecteurs propres est singulière.

    Les systèmes linéaires peuvent être décrits par

    X(0) = X0

    si le temps de départ = 0.

    Ici

    X(t) = (x0(t), …, xn(t))

    et A représente une matrice réelle de dimension (n, n). Le système linéaire peut être résolu par détermination des valeurs propres et des vecteurs propres de A. Soit S l'ensemble de tous les vecteurs propres formant une base de la totalité de l'espace à n dimensions. La transformation Y(t) = SX(t) donne

    Y(0) = SX0

    La matrice SAS–1 étant diagonale, la solution est évidente. La solution X(t) peut être déterminée par transformation inverse

    X(t) = S–1Y(t)
    Remarque Aucune sortie du temps d'exécution n'est prévue parce que l'opération principale est le calcul des vecteurs propres et des valeurs propres de la matrice A. Cette opération est négligeable pour des dimensions relativement faibles de A.

    L'illustration qui suit montre les quatre composantes de la solution de l'équation différentielle linéaire décrite par le système suivant :

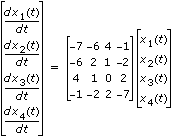
    avec

    x1(0) = 1 x2(0) = 2 x3(0) = 3 x4(0) = 4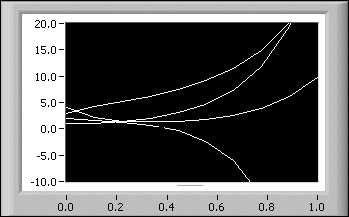

    La liste de paramètres suivante indique comment entrer les équations précédentes sur la face-avant :

    • A : [-7, -6, 4, 1; -6, 2, 1, -2; 4, 1, 0, 2; -1, -2, 2, -7]
    • X0 : [1, 2, 3, 4]
    • temps de départ: 0,00
    • temps final: 1,00