ANOVA 3D
- Mise à jour2025-07-30
- Temps de lecture : 11 minute(s)
Prend un tableau d'observations expérimentales réalisées à différents niveaux de trois facteurs et effectue une analyse trilatère de la variance.

Entrées/Sorties
 Niveaux
—
Niveaux
—
Niveaux est un cluster de trois valeurs numériques correspondant au nombre de niveaux dans les facteurs A, B et C ainsi qu'aux effets des facteurs A, B et C (fixes ou aléatoires).
 X
—
X
—
X contient toutes les données d'observation.  Indice A
—
Indice A
—
Indice A contient le niveau du facteur A auquel l'observation correspondante appartient.  Indice B
—
Indice B
—
Indice B contient le niveau du facteur B auquel l'observation correspondante appartient.  Indice C
—
Indice C
—
Indice C contient le niveau du facteur C auquel l'observation correspondante appartient.  observations par cellule
—
observations par cellule
—
observations par cellule est égal au nombre d'observations dans chaque cellule. Il en est de même pour toutes les cellules.  Info
—
Info
—
Info est une matrice 8 x 4 organisée, où la première colonne correspond aux sommes des carrés (ss) associées aux facteurs respectifs (A, B, C), aux interactions respectives (AB, AC, BC, ABC) et à l'erreur résiduelle. La deuxième colonne correspond aux degrés de liberté (dof) respectifs. La troisième colonne correspond aux moyennes quadratiques (ms) respectives. La quatrième colonne correspond aux valeurs de F respectives.   Signification
—
Signification
—
Signification est un cluster de sept valeurs numériques correspondant aux niveaux de signification.
 erreur
—
erreur
—
erreur renvoie toute erreur ou mise en garde générée par le VI. Vous pouvez câbler erreur au VI Convertir un code d'erreur en cluster d'erreur pour convertir le code d'erreur ou la mise en garde en cluster d'erreur. |
Dans toute analyse de variance (ANOVA), vous recherchez l'évidence que les facteurs ou les interactions parmi les facteurs ont un effet significatif sur les résultats expérimentaux. Ce qui varie avec chaque modèle n'est autre que la méthode utilisée pour ce faire.
Effets d'ANOVA 3D fixés et aléatoires
Un facteur correspond à un effet aléatoire s'il possède une importante population de niveaux à propos desquels vous désirez émettre des conclusions mais tels que vous ne puissiez pas échantillonner à partir de tous les niveaux. C'est pourquoi vous échantillonnez les niveaux de manière aléatoire et espérez pouvoir effectuer une généralisation à tous les niveaux. Un facteur correspond à un effet si vous pouvez échantillonner à partir de tous les niveaux à propos desquels vous désirez émettre des conclusions.
Modèle statistique d'ANOVA 3D
Soit l'équation xpqrs la sième observation aux pième, qième et rième niveaux de A, B et C, respectivement, où s = 0, 1, ..., L – 1. Exprimez chaque observation en tant que somme de huits composants. Par conséquent,
xpqrs = µ + αp + βq + γr + (αβ)pq + (αγ)pr + (βγ)qr + (αβγ)pqr + εpqrsoù :
- µ est la moyenne générale.
- αp est l'effet moyen dupième niveau du facteur A.
- βq est l'effet moyen duqème niveau du facteur B.
- γr est l'effet moyen durième niveau du facteur C.
- (αβ)pq est l'interaction bifactorielle dupième niveau du facteur A avec leqième niveau du facteur B.
- (αγ)pr est l'interaction bifactorielle dupième niveau du facteur A avec lerième niveau du facteur C.
- (βγ)qr est l'interaction bifactorielle duqème niveau du facteur B avec lerème niveau du facteur C.
- (αβγ)pqr est l'interaction à trois facteurs dupième niveau du facteur A, duqième niveau du facteur B et durième niveau du facteur C.
- εpqrs est une fluctuation aléatoire.
Hypothèses d'ANOVA 3D
Chacune des hypothèses suivantes correspond à une manière différente d'exprimer le fait qu'un facteur ou qu'une interaction parmi des facteurs n'a aucun effet sur les résultats expérimentaux. Ce VI considère qu'il n'existe aucun effet et recherche un élément permettant de contredire cette supposition. Voici les sept hypothèses :
- (A) que αp = 0 pour tous les niveaux p si le facteur A est fixe, et queσA²= 0 si le facteur A est aléatoire.
- (B) que βq = 0 pour tous les niveaux q si le facteur B est fixe, et queσB²= 0 si le facteur B est aléatoire.
- (C) que γr = 0 pour tous les niveaux r si le facteur C est fixe, et queσC²= 0 si le facteur B est aléatoire.
- (AB) que (αβ)pq = 0 pour tous les niveaux p et q si les facteurs A et B sont fixes, et queσAB²= 0 si le facteur A ou B est aléatoire.
- (AC) que (αγ)pr = 0 pour tous les niveaux p et q si les facteurs A et C sont fixes, et queσAC²= 0 si le facteur A ou C est aléatoire.
- (BC) que (βγ)qr = 0 pour tous les niveaux p et q si les facteurs B et C sont fixes, et queσBC²= 0 si le facteur B ou C est aléatoire.
- (ABC) que (αβγ)pqr = 0 pour tous les niveaux p, qet r si les facteurs A, B et C sont fixes, et queσABC²= 0 si l'un des facteurs A, B ou C est aléatoire.
Hypothèses d'ANOVA 3D
Le VI ANOVA 3D fait les hypothèses suivantes :
- Supposons que pour chaque p, qet r, εpqrs est normalement distribué avec une moyenne de 0 et une variance deσe².
- Si un facteur A est fixé, supposons que les populations de mesures à chaque niveau de A sont normalement distribuées avec une moyenne αp + µ et une varianceσA²et que toutes les populations à chacun des niveaux ont la même variance. En outre, supposons que αp sont égaux à zéro. Des suppositions semblables sont faites à propos de B et C.
- Si un facteur A est aléatoire, supposons que l'effet du niveau de A lui-même, αpest une variable aléatoire normalement distribuée de moyenne 0 et de varianceσA². Des suppositions semblables sont faites à propos de B et C.
- Si certains des facteurs, tels que A et B, associés à l'effet d'une interaction sont (αβ)pq fixes, supposons que les populations de mesures à chaque niveau de A et B sont normalement distribuées avec une moyenne µ + αp + βq + (αβ)pq et de varianceσAB². Pour tout pfixé, les moyennes (αβ)pq sont égales à zéro lorsque l'on fait la somme de tous les q. De même, pour tout qfixé, (αβ)pq sont égales à zéro lorsqu'on les additionne sur tous les p.
- Si l'un des facteurs, tels que A et B, associés à l'effet d'une interaction (αβ)pq sont aléatoires, supposons que l'effet est une variable aléatoire Normalement distribuée de moyenne 0 et de varianceσAB². Si A est fixe et B aléatoire, supposons que pour tout qfixe, les moyennes (αβ)pq sont égales à zéro lorsqu'on les additionne sur tous les p. De même, si B est fixe et A aléatoire, supposons que pour tout p fixé, les moyennes (αβ)pq sont égales à zéro lorsqu'on les additionne sur l'ensemble des q.
- On considère que tous les effets pris comme des variables aléatoires sont mutuellement indépendants.
Méthode générale d'ANOVA 3D
Dans chacun des modèles, le VI effectue une distribution de la somme totale des carrés, tss, une mesure de la variation totale des données provenant de la moyenne de la population générale, en un nombre de sommes de composants des carrés.
tss = ssa + ssb + ssc + ssab + ssac + ssbc + ssabc + sseChaque composant dans la somme tss est une mesure de la variation attribuée à un certain facteur ou à l'interaction entre les facteurs. Ici, ssa correspond à une mesure de la variation due au facteur A ; ssb correspond à une mesure de la variation due au facteur B ; ssc correspond à une mesure de la variation due au facteur C ; ssab correspond à une mesure de la variation due à l'interaction entre les facteurs A et B ; et ainsi de suite pour ssac, ssbc et ssabc. De plus, sse correspond à une mesure de la variation due à une fluctuation aléatoire. Le VI divise chacune d'entre elles par leurs propres degrés de liberté afin d'obtenir les moyennes correspondantes msa, msb, msc, msab, msac, msbc, msabc et eqm. Si, par exemple, le facteur A est à l'origine d'un puissant effet sur les observations expérimentales, alors msa sera relativement important.
Test des hypothèses d'ANOVA 3D
Pour chaque hypothèse, le VI calcule un nombre f qui est utilisé pour calculer la probabilité sig associée. Par exemple, pour l'hypothèse (A), selon laquelle (p = 0 pour tous les niveaux p), (A fixé), le VI calcule

alors
sigA = Prob{Fa – 1, abc(L – 1) > fa}où
Fa – 1, abc(L – 1)est une distribution F avec les degrés de liberté a – 1 et abc(L – 1). Vous pouvez alors utiliser les probabilités sigA, sigB, sigC et sigAB, ..., sigABC pour déterminer quand vous devez rejeter les hypothèses associées (A), (B), (C), (AB), ..., (ABC).
Comment savoir s'il faut rejeter l'hypothèse nulle ? Pour chaque hypothèse, vous devez choisir un niveau de signification. Ce niveau de signification représente la probabilité que vous voulez avoir de rejeter par erreur l'hypothèse (un choix courant est 0,05). Comparez votre niveau retenu de signification avec la sortie de la probabilité sig associée. Si la probabilité sig est inférieure au niveau de signification retenu, vous devez rejeter l'hypothèse nulle. Par exemple, si A est un effet aléatoire, que votre niveau de signification est de 0,05 et que sigA = 0,03, vous devez rejeter l'hypothèse selon laquelleσA²= 0 et conclure que le facteur A a un effet sur les observations expérimentales.
Avec certains modèles, il n'existe aucun test approprié pour certaines hypothèses. Si tel est le cas, les paramètres de sortie directement impliqués dans le test de ces hypothèses sont –1,0.
Formules d'ANOVA 3D
Soit xpqrs la sième observation aux pième, qième et rième niveaux de A, B et C respectivement, où s = 0, 1, ..., L – 1.
Soit
a = |niveaux A|
b = |niveaux B|
c = |C niveaux|
alors



















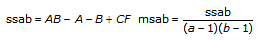



 sig A
—
sig A
—