Effectue l'intégration discrète du signal échantillonné X.


icon

Entrées/Sorties

  • c1ddbl.png X —

    X est le signal échantillonné du temps 0 à n – 1 où n est le nombre d'éléments dans X.

  • c1ddbl.png Condition initiale —

    Condition initiale spécifie la condition initiale de X dans le calcul d'intégration.

    Si la méthode d'intégration est la règle du trapèze ou la règle de Simpson, le VI utilise le premier élément de la condition initiale pour calculer l'intégration. Si la méthode d'intégration est la règle des 3/8 de Simpson ou la règle de Bode, le VI utilise les deux premiers éléments de la condition initiale pour calculer l'intégration. La valeur par défaut est [0].

  • c1ddbl.png Condition finale —

    Condition finale spécifie la condition finale de X dans le calcul d'intégration.

    Si méthode d'intégration est Règle trapézoïdale, le VI ignore Condition finale. Si la méthode d'intégration est la règle de Simpson ou la règle des 3/8 de Simpson, le VI utilise le premier élément de la condition finale pour calculer l'intégration. Si méthode d'intégration est Règle de Bode, le VI utilise les deux premiers éléments de Condition finale pour calculer l'intégration. La valeur par défaut est [0].

  • cdbl.png dt —

    dt est l'intervalle d'échantillonnage et doit être supérieur à 0. La valeur par défaut est 1,0.

    Si dt est inférieur ou égal à 0, le VI définit Intégrale de X comme un tableau vide et renvoie une erreur.

  • ci32.png méthode d'intégration —

    méthode d'intégration spécifie la méthode à utiliser pour effectuer l'intégration numérique.

    0Règle trapézoïdale
    1Règle de Simpson (valeur par défaut)
    2Règle de Simpson 3/8
    3Règle de Bode
  • i1ddbl.png Intégrale de X —

    Intégrale de X est l'intégrale discrète de X.

  • ii32.png erreur —

    erreur renvoie toute erreur ou mise en garde générée par le VI. Vous pouvez câbler erreur au VI Convertir un code d'erreur en cluster d'erreur pour convertir le code d'erreur ou la mise en garde en cluster d'erreur.

    • Intégrale de x(t) calcule une intégrale définie. La valeur du tableau en sortie associé à toute valeur x correspond à l'aire sous la courbe du tableau en entrée entre 0 et x.

    L'intégrale F(t) d'une fonction f(t) se définit comme suit :

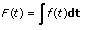
    Supposons que y représente la séquence de sortie échantillonnée intégrale de X.

    Si méthode d'intégration est Règle trapézoïdale, le VI obtient les éléments de y en utilisant l'équation suivante :

    pour i = 0, 1, 2, …, n – 1,

    n étant le nombre d'échantillons de X et x–1 étant le premier élément de Condition initiale.

    Si méthode d'intégration est Règle de Simpson, le VI obtient les éléments de y en utilisant l'équation suivante :

    pour i = 0, 1, 2, …, n – 1,

    n étant le nombre d'échantillons de X, x–1 étant le premier élément de Condition initiale, et xn étant le premier élément de Condition finale.

    Si méthode d'intégration est Règle de Simpson 3/8, le VI obtient les éléments de y en utilisant l'équation suivante :

    pour i = 0, 1, 2, …, n – 1,

    n étant le nombre d'échantillons de X, x–2 et x–1 étant les premier et second éléments de Condition initiale, et xn étant le premier élément de Condition finale.

    Si méthode d'intégration est Règle de Bode, le VI obtient les éléments de y en utilisant l'équation suivante :

    pour i = 0, 1, 2, …, n – 1,

    n étant le nombre d'échantillons de X, x–2 et x–1 étant les premier et second éléments de Condition initiale, et xn et xn + 1 étant les premier et second éléments de Condition finale.

    La Condition initiale et la Condition finale minimisent l'erreur globale en augmentant la précision aux limites, notamment lorsque le nombre d'échantillons est petit. La précision est meilleure si les conditions aux limites sont déterminées avant le calcul.

    Exemples

    Reportez-vous aux exemples de fichiers inclus avec LabVIEW suivants.

    • labview\examples\Mathematics\Probability and Statistics\Probability Density.vi