Defines the boundary condition of partial differential equations. You must manually select the polymorphic instance to use.


icon

Inputs/Outputs

  • cfxdt.png data —

    data is a variant that passes arbitrary values to the VI.

  • cNI__PDE_lvlib_NI__PDElvclass.png PDE in —

    PDE in is the class that stores the data of the equation.

  • csvrn.png Boundary Condition —

    Boundary Condition is a strictly typed reference to the VI that implements the boundary condition.

    Create this VI by starting from the VI template located in labview\vi.lib\gmath\pde.llb\Common\1D Evolutionary PDE Func Template.vit.

  • ci32.png type —

    type specifies the type of the boundary condition.

    0Dirichlet (default)—The boundary of the domain evaluates the value of the unknown function to specify the boundary condition.
    1Neumann—The boundary of the domain evaluates the value of the normal derivative of the unknown function to specify the boundary condition.
  • ci32.png position —

    position specifies the position of the boundary condition.

    0Start X (default)—LabVIEW evaluates the boundary condition with start x from the Define PDE Domain VI.
    1End X—LabVIEW evaluates the boundary condition with end x from the Define PDE Domain VI.
  • cerrcodeclst.png error in (no error) —

    error in describes error conditions that occur before this node runs. This input provides standard error in functionality.

  • iNI__PDE_lvlib_NI__PDElvclass.png PDE out —

    PDE out returns PDE in with the boundary condition.

  • ierrcodeclst.png error out —

    error out contains error information. This output provides standard error out functionality.

    • The following table gives the definitions of a normal derivative for one-dimensional equations and for two-dimensional equations defined on a rectangular domain.

    Note If the boundary type is Neumann, you must specify the value of the normal derivative of the unknown function and not the value of derivatives along the x- or y-axes. Moreover, you cannot specify the Neumann condition on a polygonal domain.
    Position Normal Derivative (One-Dimension) Normal Derivative (Rectangular Domain)
    Start X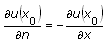
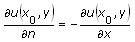    End X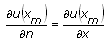
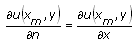    Start Y N/A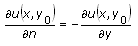
    End Y N/A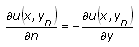

    The following block diagram is an example of defining the boundary condition for a one-dimensional wave equation. The boundary condition at Start X is Dirichlet, which the VI defines. The boundary condition at End X is Neumann, which the numeric array defines.

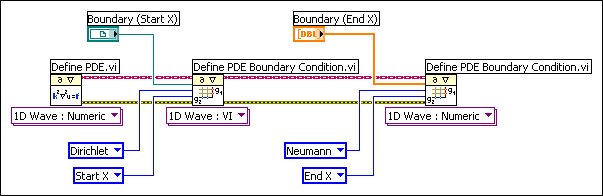
    Examples

    Refer to the following example files included with LabVIEW.

    • labview\examples\Mathematics\Differential Equations - PDE\PDE Flexible Element.vi
    • labview\examples\Mathematics\Differential Equations - PDE\PDE String Vibration.vi
    • labview\examples\Mathematics\Differential Equations - PDE\PDE Thermal Distribution.vi