Rotates a three-dimensional Cartesian coordinate system in the counterclockwise direction using the Euler angles method and returns the new coordinate of the given point. Wire data to the X input to determine the polymorphic instance to use or manually select the instance.


icon

According to Euler's rotation theory, you can describe a coordinate rotation with the Euler angles ϕ, θ, and ψ as shown below (use the default rotation order Z-X-Z as an example):

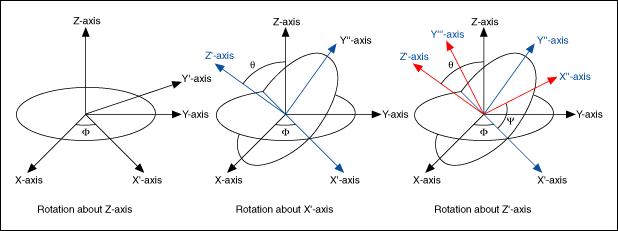
The following three steps describe the rotation:

  1. Rotate the X-, Y-, and Z-axes about the Z-axis by ϕ (–π < ϕ ≤ π), resulting in the X'-, Y'-, and Z-axes.
  2. Rotate the X'-, Y'-, and Z-axes about the X'-axis by θ (0 ≤ θ ≤ π), resulting in the X'-, Y''-, and Z'-axes.
  3. Rotate the X'-, Y''-, and Z'-axes about the Z'-axis by ψ (–π < ψ ≤ π), resulting in the X''-, Y'''-, and Z'-axes.

If you express the rotation of point (x, y, z) in terms of the following three matrices B, C, and D:

; ; ,

the coordinates, (x', y', z'), of the point in the new coordinate frame are

where A = BCD.