Berechnet die schnelle Fourier-Transformation (FFT) der Eingangsfolge X. Zur Bestimmung der Instanz des polymorphen VIs verbinden Sie Daten mit dem Eingang X oder wählen Sie die Instanz manuell aus.


icon

1D-FFT

Bei eindimensionalen Signalen berechnet das VI "FFT" anhand eines Algorithmus zur schnellen Fourier-Transformation die diskrete Fourier-Transformation (DFT) der Eingangswerte. Die 1D-DFT wird folgendermaßen berechnet:

für n = 0, 1, 2, …, N–1

wobei x die Eingangsfolge, N die Anzahl der Elemente von x und Y das Ergebnis der Transformation ist.

Der Frequenzabstand zwischen den Komponenten von Y lautet:

wobei fs die Sample-Frequenz ist.

In der Abbildung sehen Sie das Muster der Elemente in FFT {X} bei verschiedenen Einstellungen für FFT-Größe und "Verschieben?", wobei Y die FFT {X} ist und n die FFT-Größe.

n ist gerade (k = n/2)n ist ungerade (k = (n–1)/2)
Umschalttaste Array-Element Entsprechende Frequenz Array-Element Entsprechende Frequenz

FALSE

(Voreinstellung)

 Y0 DC-Komponente Y0 DC-Komponente

FALSE

(Voreinstellung)

 Y1 Δf Y1 Δf

FALSE

(Voreinstellung)

 Y2 2Δf Y2 2Δf

FALSE

(Voreinstellung)

 Y3 3Δf Y3 3Δf
⋮ ⋮ ⋮ ⋮ ⋮

FALSE

(Voreinstellung)

 Yk–2 (k-2)Δf Yk–2 (k-2)Δf

FALSE

(Voreinstellung)

 Yk–1 (k-1)Δf Yk–1 (k-1)Δf

FALSE

(Voreinstellung)

 Yk Nyquist-Frequenz Yk kΔf

FALSE

(Voreinstellung)

 Yk+1 -(k-1)Δf Yk+1 -kΔf

FALSE

(Voreinstellung)

 Yk+2 -(k-2)Δf Yk+2 -(k-1)Δf
⋮ ⋮ ⋮ ⋮ ⋮

FALSE

(Voreinstellung)

 Yn–3 -3Δf Yn–3 -3Δf

FALSE

(Voreinstellung)

 Yn–2 -2Δf Yn–2 -2Δf

FALSE

(Voreinstellung)

 Yn–1 -Δf Yn–1 -Δf
n ist gerade (k = n/2)n ist ungerade (k = (n–1)/2)
Umschalttaste Array-Element Entsprechende Frequenz Array-Element Entsprechende Frequenz
TRUE Y0 –(Nyquist-Frequenz) Y0 -kΔf
TRUE Y1 -(k-1)Δf Y1 -(k-1)Δf
TRUE Y2 -(k-2)Δf Y2 -(k-2)Δf
TRUE Y3 -(k-3)Δf Y3 -(k-3)Δf
⋮ ⋮ ⋮ ⋮ ⋮
TRUE Yk–2 -2Δf Yk–2 -2Δf
TRUE Yk–1 -Δf Yk–1 -Δf
TRUE Yk DC-Komponente Yk DC-Komponente
TRUE Yk+1 Δf Yk+1 Δf
TRUE Yk+2 2Δf Yk+2 2Δf
⋮ ⋮ ⋮ ⋮ ⋮
TRUE Yn–3 (k-3)Δf Yn–3 (k-2)Δf
TRUE Yn–2 (k-2)Δf Yn–2 (k-1)Δf
TRUE Yn–1 (k-1)Δf Yn–1 kΔf

2D-FFT

Bei zweidimensionalen Signalen berechnet das VI "FFT" die diskrete Fourier-Transformation (DFT) der Eingangsmatrix. Dazu wird die 1D-FFT der Zeilen der Matrix durchgeführt und anschließend der Spalten, die als Ergebnis der vorherigen Schrittes ermittelt wurden. Die DFT einer (M, N)-Matrix ist folgendermaßen definiert:

für u = 0, 1, ..., M-1, v=0, 1, ..., N-1

wobei x die Eingangsmatrix und Y das Ergebnis der Transformation ist.

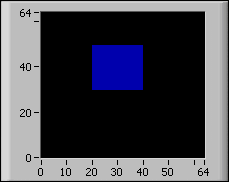
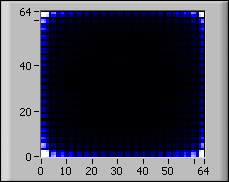
In der Abbildung ist die Wirkung von Verschieben? auf das Ergebnis der zweidimensionalen FFT noch einmal verdeutlicht:

2D-Eingangssignale FFT ohne Verschiebung FFT mit Verschiebung

Weitere Informationen

Ausgabeeinheiten der VIs mit FFT-Algorithmen

Beispiele

Die folgenden Beispieldateien sind in LabVIEW enthalten.

  • labview\examples\Signal Processing\Transforms\FFT and Power Spectrum Units.vi