Calculate Accuracy for NI Digital Multimeters
Overview
This article shows you how to calculate the accuracy of a signal for a digital multimeter (DMM). Accuracy calculations for the NI DMMs are provided below, along with examples. Sample calculations focus on DC Voltage accuracy, but the general calculation can be applied for DC current, resistance, AC voltage, and AC current.
You will need to know the following:
- Time since external calibration
- The measurement range your DMM is set to
- The magnitude of the signal reading your DMM is expecting
- Digits of resolution
Contents
PXIe-4080/4081/4082
- Determine the accuracy specification of the measurement you are taking. Refer to the accuracy tables in the Specifications document for your DMM.
PXIe-4080 Specifications
PXIe-4081 Specifications
PXIe-4082 Specifications
The accuracy specification comes in a (a + b) format, where:
a is the ppm of reading component
b is the ppm of range component
- Apply to accuracy calculation.
Accuracy = ±(ppm of reading + ppm of range)
= ±((a/1,000,000) * reading + (b/1,000,000) * range))
PXIe-4080/4081/4082 Example
Assumptions:
- Using a PXIe-4080 DMM
- Operating 90 days after calibration at 23 ºC ±5 ºC
- DMM is taking a DC Voltage signal
- DMM is set to the 10 V range and expecting a 7 V signal reading
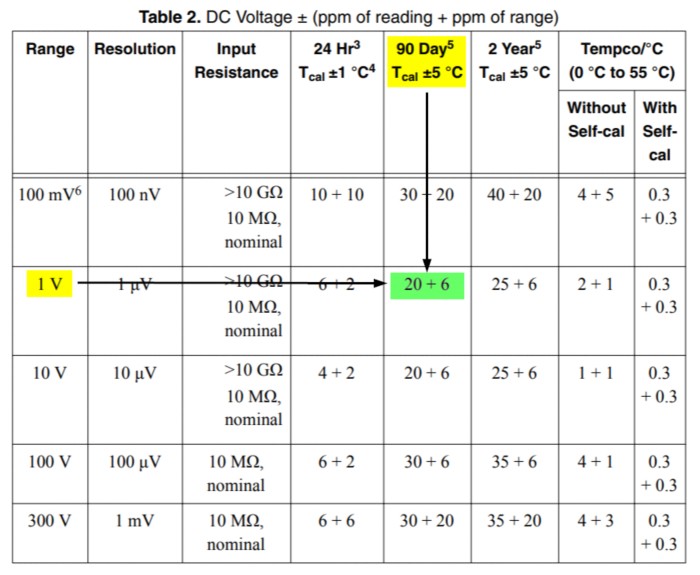
- The DC Voltage accuracy specification for 90 days after calibration and a 10 V range are:
20 + 6
or
20 ppm of reading + 6 ppm of range
DC Voltage Accuracy Specification from PXIe-4080 Specifications document
- Apply to accuracy calculation.
Accuracy = ±(ppm of reading + ppm of range)
= ±(20 ppm of reading + 6ppm of range)
= ±(20 ppm of 7 V + 6 ppm of 10 V)
= ±((7 V * (20/1,000,000) + (10 V *(6/1,000,000))
= ±200 µV
The reading should be within ±200 µV of the actual input voltage.
PXI-4070/4072
- Determine the accuracy specification of the measurement you are taking. Refer to the accuracy tables in the Specifications document for your DMM.
PXIe-4070 Specifications
PXIe-4072 Specifications
The accuracy specification comes in a (a + b) format, where:
a is the ppm of reading component
b is the ppm of range component
- Determine the additional noise error based on the DMM resolution. Refer to the Additional Noise Error table from the Specifications document for your DMM.
- Apply to accuracy calculation.
Accuracy = ±(ppm of reading + ppm of range + additional noise error ppm of range)
= ±((a/1,000,000) * reading + (b/1,000,000) * range + (additional noise error/1,000,000) * range))
PXI-4070/4072 Example
Assumptions:
- Using a PXIe-4070 DMM
- Operating 90 days after calibration at 23 ºC ±5 ºC
- Want to know accuracy at 5½-digit resolution
- DMM is taking a DC Voltage signal
- DMM is set to the 1 V range and expecting a 0.5 V signal reading
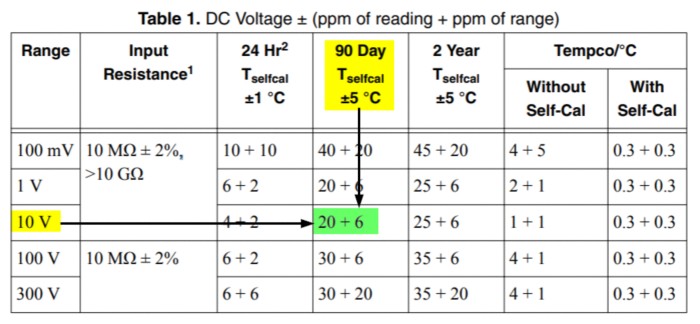
- The DC Voltage accuracy specification for 90 days after calibration and a 1 V range are:
20 + 6
or
20 ppm of reading + 6 ppm of range
DC Voltage Accuracy Specification from PXIe-4070 Specifications document
- The additional noise error specification for a 5.5-digit resolution is:
10 ppm of range
Additional Noise Error Specification from PXIe-4070 Specifications document
- Apply to accuracy calculation.
Accuracy = ±(ppm of reading + ppm of range + additional noise ppm of range)
= ±(20 ppm of 0.5 V + 6 ppm of 1 V + 10 ppm of 1 V)
= ±((0.5 V * (20/1,000,000) + (1 V * (6/1,000,000) + 1 V * (10/1,000,000))
= ±26 µV
The reading should be within ±26 µV of the actual input voltage.
PXI-4065/4071
- Determine the accuracy specification of the measurement you are taking. Refer to the accuracy tables in the Specifications document for your DMM.
PXI-4065 Specifications
PXI-4071 Specifications
The accuracy specification comes in a (a + b) format, where:
a is the ppm of reading component
b is the ppm of range component
- Determine the aperture time for your DMM and digits of resolution. To do this, open your development environment and go to Help >> NI Digital Multimeters Help >> Devices >> PXI/PCI/PCIe/USB-4065 >> DMM Measurements >> DMM Measurement Cycle >> Aperture Time.
- Determine the RMS noise (ppm of range).
Convert aperture time to number of power line cycles (NPLC) based on your country’s mains power frequency:
Mains power frequency of 60 Hz: NPLC = (aperture time/16.67 ms)
Mains power frequency of 50 Hz: NPLC = (aperture time/20 ms)
Use the Additional noise error graph in the Specifications document for your DMM to estimate the RMS noise (ppm of range) based on the NPLC.
- Determine the RMS noise multiplier based on the measurement range. Skip this step if you are using a PXI-4065. For peak-to-peak noise error, multiply the RMS noise multiplier by 6.
- Apply to calculation.
Accuracy = ±(ppm of reading + ppm of range + (RMS noise ppm of range * (RMS noise multiplier/2)))
= ±((a/1,000,000) * reading + (b/1,000,000) * range + (RMS noise * (RMS noise multiplier/2) / 1,000,000) * range))
Note: The RMS noise multiplier is divided by 2 to account for the ± of the accuracy calculation.
PXI-4065/4071 Example
Assumptions:
- Using a PXI-4071 DMM
- Operating 90 days after calibration at 23 ºC ±5 ºC
- Want to know accuracy at 5½-digit resolution
- DMM is taking a DC Voltage signal
- DMM is set to the 100 V range and expecting a 70 V signal reading
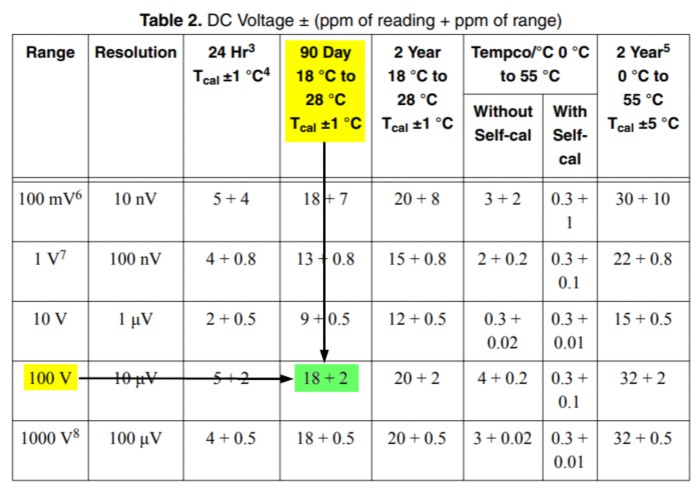
- The DC Voltage accuracy specification for 90 days after calibration and a 100 V range are:
18 + 2
or
18 ppm of reading + 2 ppm of range
DC Voltage Accuracy Specification from PXI-4071 Specifications document
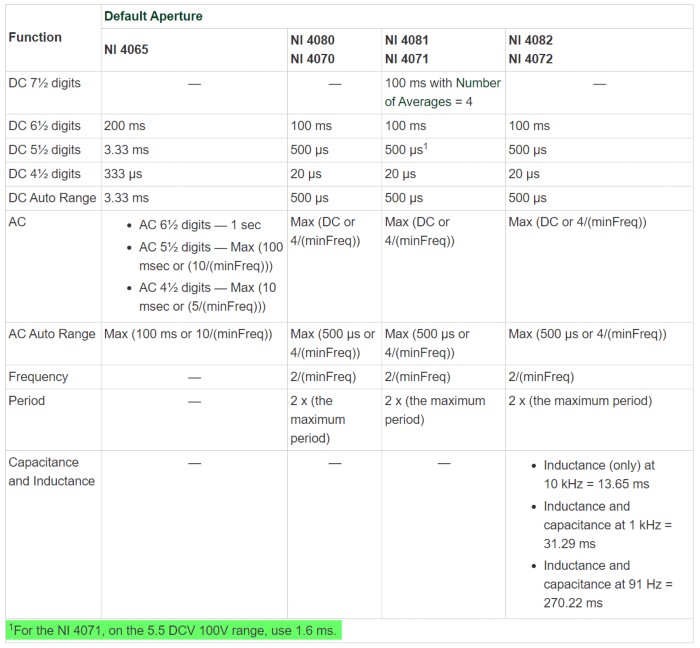
- The aperture time for the PXI-4071 with 5.5-digit resolution and 100 V range is:
1.6 ms
Aperture Time Specification for NI DMMs from NI Digital Multimeters Help
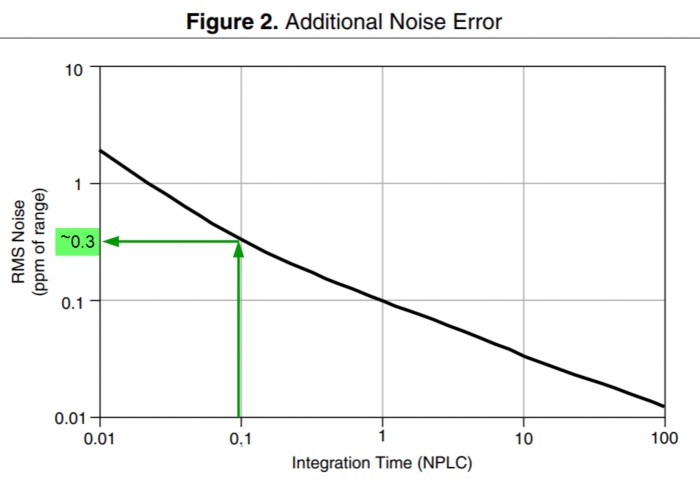
- Determine RMS noise (ppm of range).
NPLC = (aperture time/16.67 ms) (for mains power frequency of 60Hz)
NPLC = (1.6 ms)/(16.67 ms)
= 0.096
Estimate RMS Noise (ppm of range) from the Additional Noise Error graph.
RMS Noise = ~0.3 ppm of range
Additional Noise Error graph from PXI-4071 Specifications document
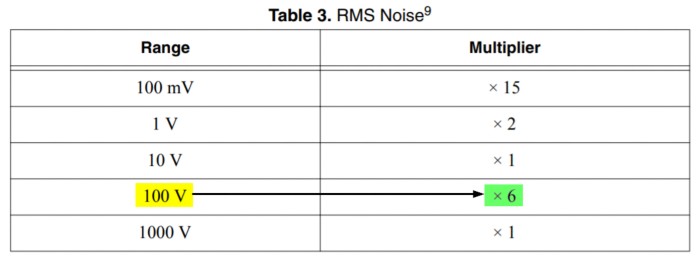
- The RMS noise multiplier for 100 V range is x6.
RMS Noise Multiplier from PXI-4071 Specifications document
- Apply to accuracy calculation.
Accuracy = ±(ppm of reading + ppm of range +(RMS noise ppm of range * RMS noise multiplier/2)
= ±(18 ppm of 70 V + 2 ppm of 100 V + (0.3 * (6/2) ppm of 100 V))
= ±(70 V * (18/1,000,000) + 100 V * (2/1,000,000) + 100 V * (0.3*3/1,000,000))
= ±1.55 mV
The reading should be within ±1.55 mV of the actual input voltage.