Understanding How TDR Works with the Digital Pattern Instrument
Overview
Contents
- Compensating for Flight Time of Signals to and from the DUT
- Effect of Reflections on Driven Signals
- Open Connection at VHDCI Connector
- Open at Far-End of the VHDCI Cable
- DUT Propagation Analysis
- Caution When Viewing Driven Signals with the Digital Scope in the DPE
Compensating for Flight Time of Signals to and from the DUT
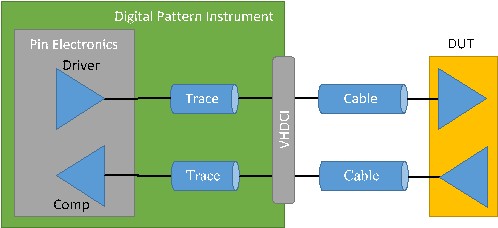
If a user wants an edge driven to the DUT at time X, the digital pattern instrument will launch that edge early so that the signal arrives at the DUT at time X. As shown in Figure 1, this means that the digital pattern instrument will start the edge early by a time equal to the propagation delay time from the pin electronics to the VHDCI connector in addition to the propagation time from the VHDCI connector through any cabling and external fixturing to the DUT. Similarly, any time that the digital pattern instrument samples a signal, it assumes that the user is concerned about the timing as if the DUT were sending the signal. This means that if an edge occurred at the DUT at time X, the digital pattern instrument would wait for the flight time (both the external cabling time plus the trace time internal to the board) for that signal to be received at the pin electronics to sample it. This is done in order to accurately represent the time when the signal left the DUT. Doing this allows the user to continue to think about timing from a DUT-centric point of view, with timing that matches how the DUT is specified.
Figure 1
Effect of Reflections on Driven Signals
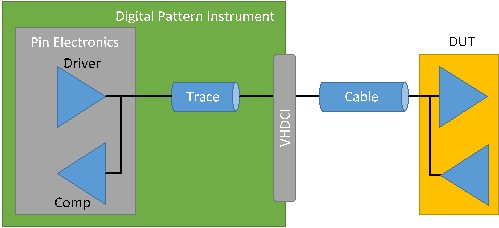
Since each channel on the digital pattern instrument is capable of bi-directional communication, each line has both a driver and a comparator on it, as shown in Figure 2. When the signal is driven from the digital pattern instrument it is reflected and captured by the comparator. At times, this can make it difficult to make sense of the timing of the driven signals, as shown in the Digital Scope, that the digital pattern instrument is sending to the DUT. In the Analysis section this document will walk through some example cases in order to make this easier to understand.
Figure 2
Open Connection at VHDCI Connector
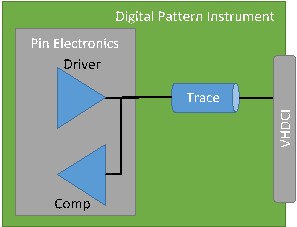
Figure 3
We will start by looking at a single channel from the digital pattern instrument driving to an open connection at the VHDCI connector on the front panel, as shown in Figure 3. An individual digital pattern instrument is calibrated for timing with the front panel as the timing calibration plane. This means that if channels have edges or strobes programmed to occur at the same time, they will be aligned at the front panel.
Note that in an STS, the timing calibration plane is at the POGO interface on the tester. Although the discussion here will generically apply to both cases, the biggest difference for the STS case is that instead of the calibration just needing to adjust for ~700 ps of delay from the pin electronics to the VHDCI connector, it will also need to account for the length of the POGO cable, which can be up to about 5 ns, but may vary depending on the length of the POGO cable.
Internal to the digital pattern instrument, there is a non-zero length trace from the pin electronics chip to the VHDCI connector. This trace is a few inches long and will have an average delay of around 700 ps, but this will vary a little from channel to channel.
When an edge is programmed to be received by the DUT at a particular time, internally the digital pattern instrument needs to launch the edge approximately 700 ps early, non-zero length internal trace, plus the additional flight time from the VHDCI connector to the DUT in order for the edge to make it to the DUT at the right time.
Similarly, for signals coming from the DUT, the sampling of the digital pattern instrument needs to accommodate for the time from the DUT to the VHDCI connector and the time from the VHDCI connector through this internal path before it is seen by the pin electronics. This means that if an edge occurred at time 50 ns at the VHDCI connector, the pin electronics would need to sample it at time ~50.7 ns to correctly show what happened at the front panel at time 50 ns.
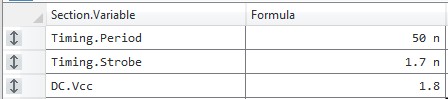
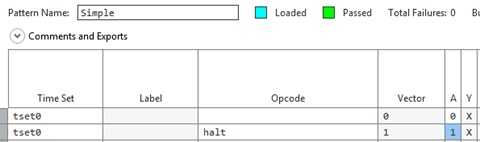
Below is an example in the Digital Pattern Editor to show what is happening. This is a basic pattern that will drive a transition on a line at time 50 ns. Figure 4, Figure 5, and Figure 6 show the specification sheet, timing sheet, and the pattern, respectively.
Figure 4
Figure 5
Figure 6
Vector 1 drives a rising edge on pin A at time 50 ns. Since it is return-to-low (RL), the line will go back low at time 75 ns.
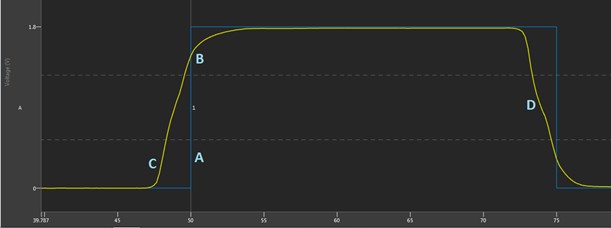
Figure 7
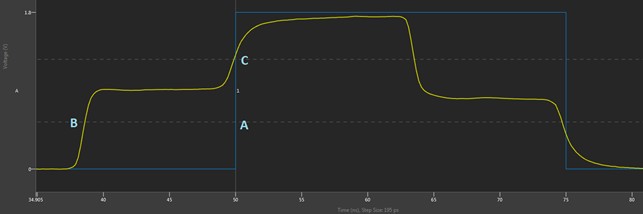
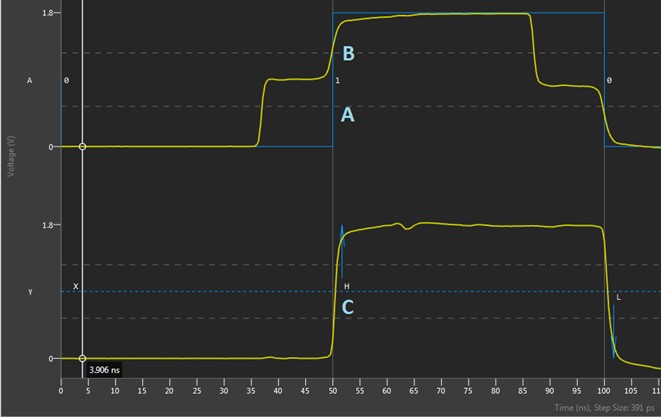
Figure 7 shows the Digital Scope after bursting the pattern. In blue (“A” in the image), the Digital Scope shows the ideal waveform with a step from 0 to 1 at time 50 ns. In yellow, we see that the signal sent from the digital pattern instrument is a 1.8 V signal, but since it has a source impedance of ~50 ohms and the transmission line is ~50 ohms, only half of this voltage propagates down the trace immediately (note that since the transmission line is shorter than the edge time, this step is not very pronounced here). When it reaches the high impedance at the end of the transmission line (at the open connection at the front panel), it will reflect, making a full 0 to 1.8 V swing at the front panel at time 50 ns. For sampling, in order to reflect this change to the user, we wait for the flight time for this reflection to get back to the pin electronics—about 700 ps after it was at the front panel. We show this to the user as what happened at the front panel at time 50 ns. You can see this at location “B” in the image, as the reflected signal has the transition up to 1.8 V at time 50 ns.
This becomes slightly more complicated when the initial step occurs at the pin electronics. We know that to drive the edge at the front panel at time 50 ns, the edge needed to be launched ~700 ps early, but it appears that the edge is being launched earlier than this (location “C” in the image). This is because for sampling we always show the signal coming back from the DUT, then adjust it to show the time that occurred at the DUT. In this case, the actual reflected signal got back to the pin electronics at time ~50.7 ns, but this corresponded to that edge at the VHDCI connection at 50 ns, so we display it there on the waveform. However, for the initial step, we needed to launch the edge at time ~49.3 ns to get the edge to the DUT at time 50 ns. Since the comparator timing is compensating to accurately represent the timing of signals at the DUT, this initial step that we drive is seen at 2 x flight time before the edge, happening close to time 48 ns in the image above.
Open at Far-End of the VHDCI Cable
Figure 8
This section will show the performance both before and after a TDR adjustment is done, taking the same case as before but adding a VHDCI cable to the system. See Figure 8 for information about how the physical system is set up.
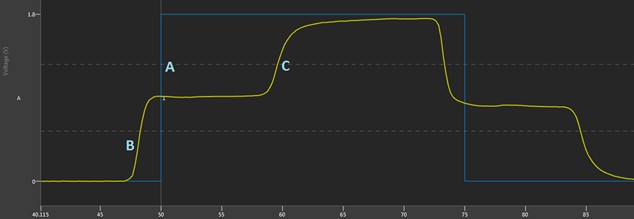
The first case will be without a TDR adjustment, as shown in Figure 9. In this case, the digital pattern instrument will still drive a rising edge at time 50 ns at the front panel (since TDR has not been applied to move the edges out to the DUT). This is still shown with the ideal wave plotted in blue (“A” in the image). Using the same reasoning from the previous case, in Digital Scope, the initial step from the driver will be seen a 2x flight time early (“B” in the image). A 1 m VHDCI cable has an electrical delay of about 5 ns, so with 2x 5 ns = 10 ns, the second step of the edge is seen at about time 58 n (“C” in the image). With the edge scheduled at time 50 ns, this does not reflect the real time that anything happened at the DUT, which is the purpose of using TDR compensation.
Figure 9
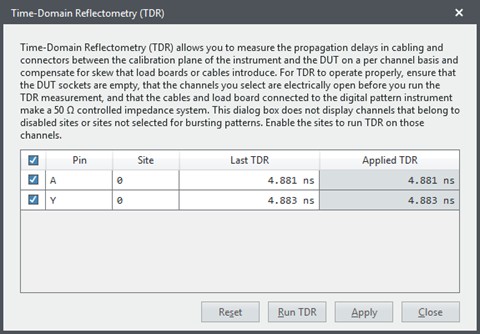
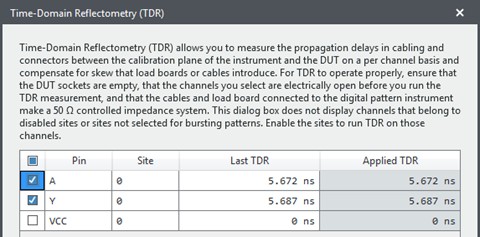
Now looking at the same physical setup, but applying TDR, we can see that it detected the electrical length of the cable to be about 4.88 ns, as shown in Figure 10. As a reminder, this means that when we drive an edge to the DUT, it will drive even earlier by the propagation delay time from the calibration plane to the DUT. Similarly, for received signals, it will sample those later by this additional propagation time.
Figure 10
Looking at the waveform from Digital Scope, as shown in Figure 11, we can see that to create the edge at time 50 ns (“A” in image), we need to send the edge early so that it arrives at the end of the cable at time 50 ns. Like the previous case, since we plot the signal received from the DUT by sampling the flight time after an edge occurred at the DUT, this has the effect of showing the initial wave front starting at 2x flight time before the edge gets there. In this case, this is (4.9 ns + 0.7 ns) x 2 = 11.2 ns (“B” in the image) before the reflected signal will come back (“C” in the image).
Figure 11
DUT Propagation Analysis
As we move on to look at a real DUT, the benefits of the timing that the Digital Scope shows should become more evident.
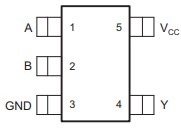
In this example, the SN74AUC1G86 single 2-input Exclusive OR gate was used, as shown in Figure 12. For simplicity, input B is tied to GND, making it act as a simple buffer.
Figure 12
This example will focus on evaluating the propagation time through the gate. The datasheet for the SN74AUC1G86, Figure 13, specs the propagation time from input A to output Y as a minimum of 0.4 ns, typical of 1.0 ns, and maximum of 1.7 ns at 1.8 V Vcc.
Figure 13
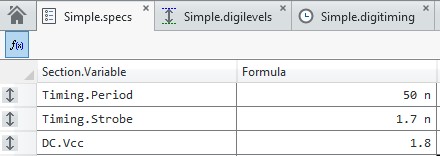
Thinking in terms of the DUT, the user can set up the specs, levels, and timing sheets in the Digital Pattern Editor as shown in Figure 14, 15, and 16, respectively.
Figure 14
The levels will be for 1.8 V. While technically the propagation delay is specified from a 50% threshold from the A/B input to a 50% threshold on the output of the DUT, since the load conditions in this example don’t match the specified conditions perfectly, the thresholds for comparing the output were set at > 70% of Vdd for an output high and < 30% of Vdd for an output low to make this simple to understand.
Figure 15
Figure 16
For this case, the digital pattern instrument is connected through a 1 m VHDCI cable to a test board that has the XOR gate on it. The digital pattern instrument needs to compensate for the flight time through the cable and the board to the DUT. The TDR function is used to calculate this flight time, as shown in Figure 17.
Figure 17
Figure 18
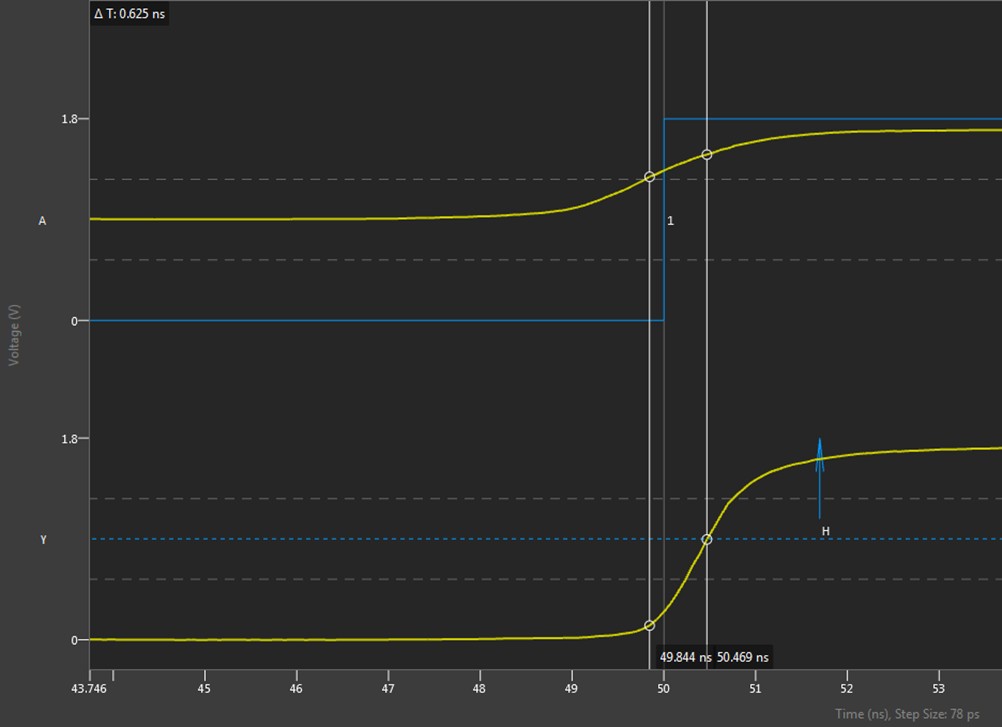
Figure 18 shows that the input to the buffer gets a rising edge at 50 ns (“A” in the image). Since the buffer has a high impedance input, the reflection that comes back from this matches the desired waveform, showing that the edge got to the buffer at 50 ns (“B” in the image).
Showing the timing of the signals received from the DUT in this manner, the user gets an easy to understand display of the signal being received from the DUT, since the timing in Digital Scope is displayed to most easily represent signals coming from the DUT. Here, the signal from the buffer can be seen coming out very shortly after the rising edge (“C” in the image above). Zooming in on this shows the propagation delay through the DUT to be about 625 ps, as shown in Figure 19.
Figure 19
If a user saw a failure in the pattern, found the failing cycle in HRAM, and then used Digital Scope to understand the reason for the failure, the display would show the exact strobe timing. In the image above, the period starts at time 50 ns and the strobe looking for an “H” on line Y is 1.7 ns later. If the strobe time needs to be changed, the time seen in Digital Scope will perfectly match the strobe time that would need to be set in the time set.
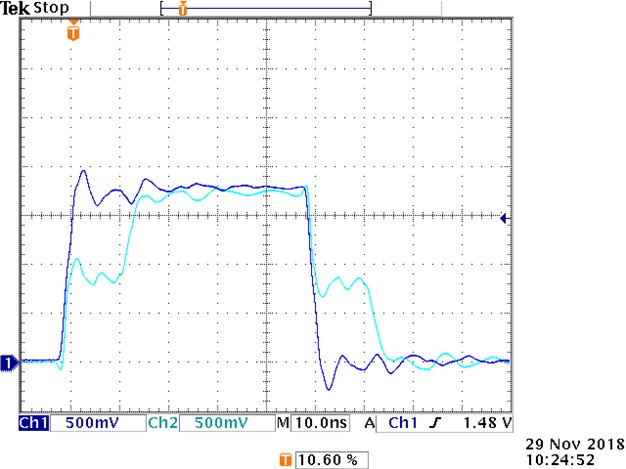
Using a box scope to probe these signals directly at the DUT as a sanity check shows that this matches what is shown above. Refer to Figure 20. The input to the buffer is shown in dark blue and the output is in light blue. The output changes in under a 10th of the time division , matching the ~675 ps delay observed at the digital pattern instrument.
Figure 20
Caution When Viewing Driven Signals with the Digital Scope in the DPE
With the most confusing signals being the ones that are driven from the digital pattern instrument to the DUT, it is probably worth noting that in cases with higher bit rates relative to the transmission line length, it is impossible to reliably make sense of what is happening at the DUT from the signal seen at the driver end.
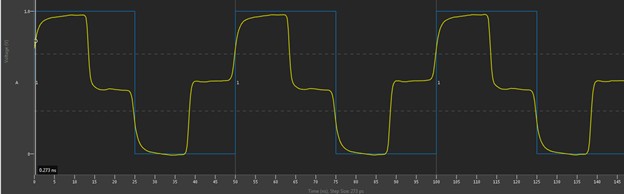
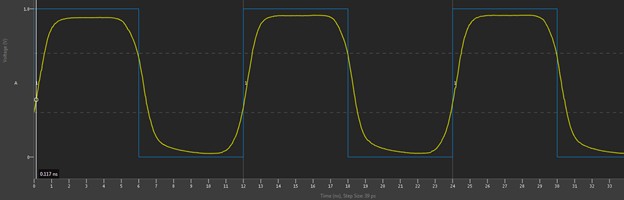
Figure 21 shows a case where it is possible to make sense of what is seen at the end of the line. This is a case of a 50% duty cycle pulse train with a period of 50 ns. The edges are far enough apart that the signal propagates to the end of the cable and back for each transition to be seen at the driver end of the transmission line.
Figure 21
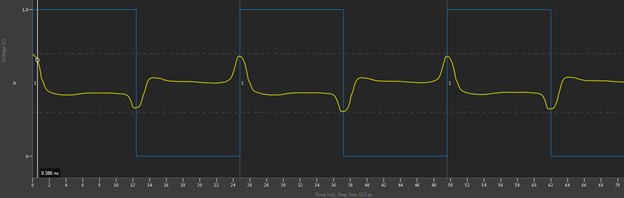
However, depending on how the reflections line up, the Digital Scope may not have such a clean view. For instance, Figure 21 shows that the round-trip flight time is about 12.4 ns (time from the initial step to the reflection coming back). If the period is changed from 50 ns to 24.8 ns, then the falling edge would be launched at the exact time that the reflected rising edge came back. At the end of the transmission line, a perfectly good square wave with a 24.8 ns period would be seen, but the driver end would barely see any signal at all, as shown in Figure 22.
Figure 22
With the same transmission line attached, there could be other cases where the programmed frequency of the signal causes the line to resonate (the reflected rising edge hits at the same time as the initial rising step from the next pulse). In this case, Digital Scope doesn’t even show a stair step at the driving side of the line, as seen in Figure 23.
Figure 23
There are many variations in between that can make it difficult to make sense of what is happening at the DUT based on what is perceived at the driver end, especially with non-repetitive and non-50% duty cycle signals.
In general, users should rely on the blue ideal waveform for driven signals, especially when trying to debug something in production. However, if you are writing a test and want to verify the driven signal then you will need to use a scope to probe at the DUT.