通过欧拉方法求解带初始条件的常微分方程。


icon

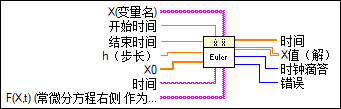
输入/输出

  • c1dstr.png X(变量名) —

    X是变量字符串数组。

  • cdbl.png 开始时间 —

    起始时间是常微分方程(ODE)的开始点。默认值为0。

  • cdbl.png 结束时间 —

    结束时间是待测时间区间的结束点。默认值为1.0。

  • cdbl.png h（步长） —

    h是固定的步长。默认值为0.1。

  • c1ddbl.png X0 —

    X0是描述开始条件的向量，x[10], …, x[n0]。

    X0和X的分量一一对应。

  • cstr.png 时间 —

    时间是时间变量的字符串表示。默认的变量为t。

  • c1dstr.png F(X,t) (常微分方程右侧 作为X和t的函数) —

    F(X,t)该一维数组用于表示微分方程的右端项。公式可包含任意数量的有效变量。

  • i1ddbl.png 时间 —

    时间是用于表示时间步长的数组。Euler方法在开始时间和结束时间之间可以产生等距的时间步长。

  • i2ddbl.png X值（解） —

    X值是解向量x[10], …, x[n]组成的二维数组。

    顶层索引是时间数组中指定的时间步长，底层索引是元素x[10], …, x[n]。

  • iu32.png 时钟滴答 —

    计时是用于计算函数值的时间，以毫秒为单位。

  • ii32.png 错误 —

    错误返回VI的任何错误或警告。使用错误的X、X0和F(X,t)输入会导致错误。将错误连接至错误代码至错误簇转换VI，可将错误代码或警告转换为错误簇。

    • 常微分方程(ODE)通常表示为：

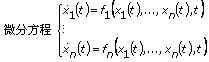
    其中

    给定函数f1, …, fn、数字和起始点t = t0。通过转换F = (f1, …, fn); X(t) = (x1(t), …, xn(t)); and X0 = (x10, …, xn0)，

    得到：

    函数必须X满足此前的方程。

    欧拉方法是最基本并且常用的常微分方程解法。以t0作为开始，采用固定并且较小的步长h，得到：

    X(t0 + h) = X(t0) +hF(X(t0), t) X(t0 +2h) = X(t0 + h) +hF(X(t0 + h),t0 + h) ⋮

    计算结果。如果 时间开始 +nh ≥ 时间结束，这个过程就停止了，其中 时间结束 是被调查的时间间隔的右端点。

    下图为常微分方程的解。

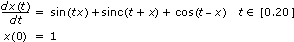
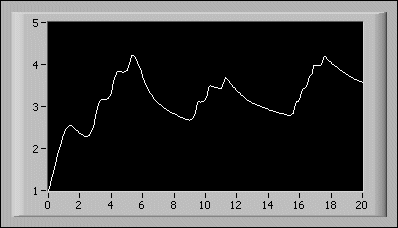
    在前面板上输入方程和初始条件：

    • 开始时间：0.00
    • 结束时间：20.00
    • X0：1.00
    • F(X,t)：sin(t*x) + sinc(t + x) + cos(t - x)
    • X：x