使用差分进化法(DE)，求解有边界约束、非线性等式约束和非线性不等式约束的全局优化方程。


icon

输入/输出

  • cfxdt.png 函数数据 —

    函数数据包含用户定义函数运行时所需的静态数据。

  • csvrn.png 目标和约束函数 —

    目标和约束函数是对VI的引用，VI可将非线性函数、非线性等式约束函数，以及非线性不等式约束函数作为独立的输出。在引用VI中，目标函数输出不能为空，但约束函数输出可选择为空。因此，等式约束输出、不等式约束输出可以分别或同时为空。

    可基于VI模板labview\vi.lib\gmath\GlobalOptimization.llb\Global Optimization_Objective Function.vit创建该VI。

  • c2ddbl.png 初始参数 —

    初始参数是最优化过程的初始参数。当开始状态为空时，LabVIEW使用初始参数。初始参数的每一行为一组参数。初始参数的列数必须等于边界中的 最小值和最大值长度。

    如果初始参数的行数小于种群规模，LabVIEW初始化剩余参数。如果初始参数的行数大于种群规模，LabVIEW将忽略多余参数。

  • ccclst.png 边界 —

    边界该簇包含正在最优化处理的参数的数值上下界。

  • c1ddbl.png 最小值 —

    最小值包含正在被最优化处理的参数的最低允许值。最小值不能为空。最小值的长度必须等于最大值的长度。最小值不接受例外值（例如，Inf、–Inf或NaN）。

  • c1ddbl.png 最大值 —

    最大值包含正在被最优化处理的参数的最高允许值。最大值不能为空。最大值的长度必须等于最小值的长度。最大值不接受例外值（例如，Inf、–Inf、NaN）。

  • ccclst.png 开始状态 —

    开始状态包含了Pareto索引和参数的初始值。开始状态通常是上一次优化的结束状态，并作为优化的预热开始。如果开始状态被赋值，LabVIEW忽略初始参数。

  • c1dcclst.png 种群 —

    种群包含了一组参数，这些参数包含了参数、对象函数、等式约束、不等式约束和基本索引的值。

  • c1ddbl.png 参数 —

    参数包括备选参数值。

  • c1ddbl.png 目标函数 —

  • c1ddbl.png 等式约束 —

  • c1ddbl.png 不等式约束 —

  • c1di32.png Pareto索引 —

    Pareto索引包含了在所有备选参数中进行选择的索引。

  • cerrcodeclst.png 错误输入（无错误） —

    错误输入表明该节点运行前发生的错误条件。该输入提供标准错误输入功能。

  • cnclst.png DE设置 —

    DE设置包含了针对差分进化(DE)方法的附加设置。

  • ci32.png 种群规模 —

    种群规模是优化过程的每次循环迭代中，LabVIEW计算的候选参数组的数量。该规模是优化过程的每次循环迭代中，对象函数调用的数量。更大的种群规模通常产生更好的优化结果和更长的执行时间。默认值为10。

  • cdbl.png 缩放因子 —

    缩放因子是LabVIEW使用生成变异参数的多样因子。缩放因子的值越大，变异参数的多样性就越大。默认值为0.9。

  • cdbl.png 交叉概率 —

    交叉概率是LabVIEW从变异参数中继承实验参数的概率。交叉概率的值越大，LabVIEW接受变异参数的概率就越大。默认值为0.95。

  • cu16.png 边界映射方法 —

    边界映射方法是LabVIEW将实验参数映射至边界的方法。

    0无
    1边界和值之间的随机数（默认）
    2重新初始化
  • cu16.png 变异方法 —

    变异方法是LabVIEW生成变异参数的方法。

    0随机（默认）
    1二选一
    2偏向最优
    3当前和最优之间
  • cu16.png 交叉方法 —

    交叉方法是LabVIEW使备选参数与变异参数交叉的方法。

    0均匀（默认）
    1指数
  • cnclst.png 停止标准 —

    停止标准是终止最优化过程的条件的集合。

  • ci32.png 最大循环次数 —

    最大循环次数是优化过程的最大循环次数。如循环数超过最大循环次数，最优化将停止。默认值为50。

  • ci32.png 最多函数调用 —

    最多函数调用是停止最优化过程之前允许的最多目标函数调用次数。默认值为-1。

    -1表示优化过程永不停止且不依赖目标函数调用次数。决定目标函数调用实际次数的公式为：种群规模×（最大循环次数 + 1）。

  • cdbl.png 最大时间（秒） —

    最大时间（秒）是LabVIEW允许的从最优化过程开始到结束的最大时间。默认值为-1。-表示优化过程永不超时。

  • ii32.png 函数调用次数 —

    函数调用次数是在最优化过程中目标函数调用的次数。

    如果最多函数调用为-1，最多函数调用等于种群规模×（最大循环次数+1）。

  • i1ddbl.png 最小值 —

    最小值是在可能的全部最小值中的确定的全局最小值。

  • i1ddbl.png F（最小值） —

    F（最小值）是目标函数在最小值处的取值。

  • icclst.png 结束状态 —

    结束状态包含了优化过程结束时的Pareto索引和种群的最终值。

  • i1dcclst.png 种群 —

    种群包含了一组参数，这些参数包含了优化过程结束时的备选参数、对象函数、等式约束、和不等式约束的值。

  • i1ddbl.png 参数 —

    参数包括优化过程结束时的备选参数值。

  • i1ddbl.png 目标函数 —

    目标函数包含了在参数的目标函数值。

  • i1ddbl.png 等式约束 —

    等式约束包含了在参数的等式约束值。

  • i1ddbl.png 不等式约束 —

    不等式约束包含了在参数的不等式约束值。

  • i1di32.png Pareto索引 —

    Pareto索引包含了在所有备选参数中进行选择的索引。

  • ierrcodeclst.png 错误输出 —

    错误输出包含错误信息。该输出提供标准错误输出功能。

    • 该VI通过找到x，最小化f(x)来求解全局优化方程，约束如下：

    边界约束min ≤ x ≤ max
    等式约束g(x) = 0
    不等式约束h(x) ≤ 0

    x是要优化的参数集合。f(x)是要最小化的目标函数集合。该问题中，等式约束和不等式约束是可选的。

    差分进化法是解全局优化方程的一种方法。差分进化算法对初始参数进行反复变异和交叉，逼近实际的全局优化值。

    注： 差分进化法不保证找到全局优化值。最优返回参数取决于差分优化法的选择和问题本身。

    如目标函数求解的过程较长，差分进化法需要多次调用目标函数。调用的次数取决于样本大小，以及优化过程中每个循环的处理速度。该VI使For循环能实现并行执行，使LabVIEW能充分运用多核处理的优势。如实现并行循环，需执行下列操作：

    • 将实现目标函数的VI改为共享副本的可重入VI。
    • 打开引用时使用参数0x40，如下图所示。

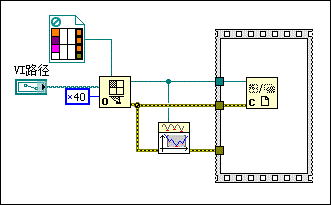
    下图显示了VI如何解全局优化方程。

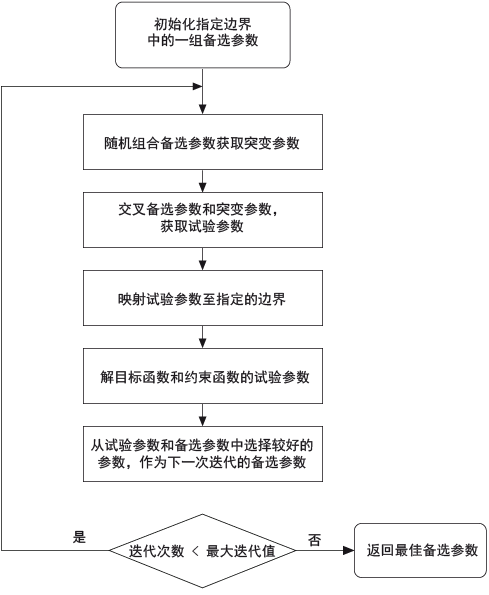
    范例

    请参考LabVIEW附带的下列范例文件。

    • labview\examples\Mathematics\Optimization\Find Global Min on Surface.vi
    • labview\examples\Mathematics\Optimization\Two Circles Optimization.vi