计算实数多项式P(x)在实数区间上的零点个数，区间由首端和末端确定，不能给出零点的值。


icon

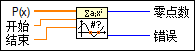
输入/输出

  • c1ddbl.png P(x) —

    P(x)是用于表示多项式的数组。该数组的第一个系数与P(x)的常系数有关。

  • cdbl.png 开始 —

    开始是区间最左侧的点。默认值为0.0。

  • cdbl.png 结束 —

    结束是区间最右侧的点。默认值为0.0。

  • ii32.png 零点数 —

    零点数是区间（开始，结束）之间P(x)零点的准确数量。

  • ii32.png 错误 —

    错误返回VI的任何错误或警告。如开始>结束，应用程序可视为错误。将错误连接至错误代码至错误簇转换VI，可将错误代码或警告转换为错误簇。

    • 这个VI使用Sturm算法来计算零的数量。Sturm算法可处理两种情况。p(x)为x中的实数多项式，p'(x)为p(x)的导数。如d(x)为p(x)和p'(x)的最大公因式，

    d(x) = gcd(p(x), p´(x))

    d(x)不是常量时，p(x)有多个零点。即，多项式p(x)/d(x)只有单个零点。

    按照这种想法，使多项式p(x)作为多个仅有单根的多项式的乘积，每个多项式只有单重实数零点。p(x)的零点数量等于已定义的多项式（只有单个零点）的零点的总和。

    如需确定只有单个零点的实数多项式p(x)的零点个数，可使用下列算法：

    p(x) =q1(x)p1(x) -p2(x) p1(x) =q2(x)p2(x) -p3(x) ⋮ pr - 2(x) =qr - 1(x)pr - 1(x) - pr(x)

    Stum Chain

    (p(x), p1(x), …, pr(x))

    可确定两个值W(首端)和W(末端)。W(x)是Stum Chain中符号改变的次数

    (p(x), p1(x), …, pr(x))

    p(x)的零点总数等于W(末端)–W(首端)。

    注：

    如果你对一个实数多项式的所有实数零点感兴趣，选择

    开始 =-max{(|a0|+...+|an-1|)/|an|, 1}

    和 结束 =最大{(|a0|+...+|an-1|)/|an|, 1}

    其中a0,a1, ..., an 是多项式的元素。