一元数值积分
- 更新时间2025-07-30
- 阅读时长4分钟
通过四个常用积分方法中的某个对输入数组进行数值积分。
可通过连线数据至输入数组输入端确定要使用的多态实例,也可手动选择实例。
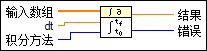
输入/输出
 输入数组
—
输入数组
—
输入数组包含要进行积分的数据,可通过在多个dt对已经积分的f(t)进行采样得到,f(0), f(dt), f(2dt),…。  dt
—
dt
—
dt是间隔的大小,用于表示获取函数的输入数组中数据的采样步长。 如dt为负数,VI使用绝对值。  积分方法
—
积分方法
—
积分方法指定进行数值积分的方法。
 结果
—
结果
—
结果返回数值整数。  错误
—
错误
—
错误返回VI的任何错误或警告。将错误连接至错误代码至错误簇转换VI,可将错误代码或警告转换为错误簇。 |
连线至该VI的x值必须是均匀分割的,否则结果不正确。如需连线至该VI的x值不均匀分布,可使用不平均数值积分VI计算积分。
一元数值积分
| 点数 | 分方法计算 |
|---|---|
| 224 | 55 Bode, 1 Simpsons' 3/8 |
| 225 | 56 Bode |
| 226 | 56 Bode, 梯形 |
| 227 | 56 Bode, 1 Simpsons' |
| 228 | 57 Bode, 1 Simpsons' 3/8 |
如有224个点并且选择Bode方法,VI可通过55个Bode方法和1个Simpsons 3/8方法得到结果。
采样间隔(dt)可确定要使用的方法,然后依据相邻点的数量按照不同方法计算,通过连续应用基本公式计算积分。每种方法中使用的点数可反映方法的阶数。结果是每种方法计算后的连续和。

j取决于点的数量和积分方法。
下面列出了用于计算部分和的基本公式,按升序排列:
- 梯形:1/2(x[i] + x[i + 1])*dt
- Simpsons':(x[2i] + 4x[2i + 1] + x[2i + 2])*dt/3, k = 2
- Simpsons' 3/8:(3x[3i] + 9x[3i + 1] + 9x[3i + 2] + 3x[3i + 3]) * dt/8, k = 3
-
博德:(14x[4i] +64x[4i + 1] +24x[4i + 2] +64x[4i + 3] +14x[4i + 4]) * dt/45, k = 4
对于 i =0,1,2,3,4,...,[(N -1)/k]的积分部分
其中,N是数据点的数量,k是与方法相关的整数,x是输入数组。
注: 如为某个方法提供的点的数量没有包含整数个部分和,该方法可用于所有可能的点。其余点将使用该方法以下的适用方法。例如,如选择Bode方法,前述例子表明了该VI对于不同数量点的计算。