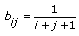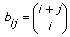依据矩阵类型创建特殊的矩阵。连线至输入向量2和输入向量1输入端的数据类型可确定要使用的多态实例。


icon

输入/输出

  • c1dcdb.png 输入向量2 —

    输入向量2在某些选项中该输入可用于创建特殊矩阵。

  • ci32.png 矩阵类型 —

    矩阵类型指定生成的特殊矩阵的类型，该VI使用该类型生成特殊矩阵输出。

    如n为矩阵大小，X为输入向量1，则nx为X的大小，Y为输入向量2，则ny为Y的大小，B表示特殊矩阵。

    0单位－生成n行n列的单位矩阵。
    1对角－生成一个nx行nx列的对角矩阵，对角元素为X的元素。
    2Toeplitz－生成nx行ny列的Toeplitz矩阵，X为第一列，Y为第一列。如X和Y的第一个元素不同，则使用第一个X元素。
    3

    范德蒙德-生成一个nx-by-nx 的范德蒙德矩阵，该矩阵的列是 X 元素的幂。范德蒙矩阵中的元素为：

    bi,j = xinx – j – 1

    i,j = 0…nx – 1。

    4

    伴随－生成一个nx-1行nx-1列的伴随矩阵。如向量X是多项式系数的向量，则X的第一个元素为最高阶的系数，最后一个元素是多项式的常项，相应的伴随矩阵按如下方式构建。第一行是

    从第二行开始余下的B是单位矩阵。

    伴随矩阵的特征值包含相应多项式的根。

    5Hankel－生成一个nx行ny列的Hankel矩阵，X为第一列，Y为最后一行。如Y的第一个元素和X的最后一个元素不同，该VI使用最后一个X元素。
    6Hadamard－生成n行n列的Hadamard矩阵，元素为1和-1。所有的列或行彼此正交。矩阵大小必须为2的幂、2的幂与12相乘或2的幂与20相乘。当n为1时，该VI返回空矩阵。
    7Wilkinson－生成n行n列的Wilkinson矩阵，矩阵特征值示病态的。
    8

    Hilbert－生成一个n行n列的Hilbert矩阵，矩阵成员遵循下面等式。

    i,j = 0，1…n – 1。

    9逆Hilbert－生成n行n列的逆Hilbert矩阵。
    10Rosser－生成8行8列的Rosser矩阵，矩阵的特征值是病态的。
    11

    Pascal－生成一个n行n列的对称Pascal矩阵，矩阵成员遵循下面等式。

    i,j = 0，1…n – 1。

  • ci32.png 矩阵大小 —

    矩阵大小确定输出的特殊矩阵的维数。

  • c1dcdb.png 输入向量1 —

    输入向量1在某些选项中该输入可用于创建特殊矩阵。

  • i2dcdb.png 特殊矩阵 —

    特殊矩阵是生成的矩阵。

  • ii32.png 错误 —

    错误返回VI的任何错误或警告。将错误连接至错误代码至错误簇转换VI，可将错误代码或警告转换为错误簇。

    • 范例

    请参考LabVIEW附带的下列范例文件。

    • labview\examples\Mathematics\Linear Algebra\Matrix to a Power.vi