计算Pearson χ²独立性测试。该函数可用于判断列联表的行和列分类变量是否独立。


icon

输入/输出

  • c2di32.png 表格 —

    表格是计数或频率的输入列联表。

  • idbl.png x —

    x是计算的Pearson's χ²测试统计。

  • idbl.png 概率 —

    概率或p值返回观察采样统计（与测试统计程度相同）的概率。如果该值小于期望的重要级，应该推断出行变量和列变量之间存在一定的关系。

  • ii32.png 错误 —

    错误返回VI的任何错误或警告。将错误连接至错误代码至错误簇转换VI，可将错误代码或警告转换为错误簇。

    • 应变表六使用同质性的χ²检验和独立性的χ²检验来检验你的假设。在检验假设之前，应确定每个测试的概率的最小值。概率的最小值可确定是否接受假设。通常，概率选取的值较小。一般选择0.05。如VI返回的实际概率值小于确定的值，可拒绝假设。

    在同质性的χ²检验中，VI从一个分类方案中的每个类别中随机抽取某个固定规模的样本。对于每个采样，VI依据第二个模式对检验对象分类并加以标记。VI通过对假设进行检验，确定从中获取采样的总体的分布（根据第二个分类模式）是否一致。

    对于χ²独立性检验，VI只从总人口中抽取一个样本。然后，VI对每个对象进行分类并在两个分类模式中对其进行标记。VI可对分类模式独立的假设进行检验。

    公式

    如yp, q是列联表中第(pq)个单元格中的发生次数

    p = 0, 1, …, (s – 1) and q = 0, 1, …, (k – 1)，

    s是列联表格中的行数，k是列联表格中的列数。

    如

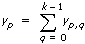
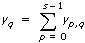
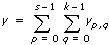
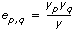
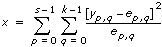
    VI通过x计算概率。

    p =Prob {X ≥ x}

    其中 X 是一个来自χ²分布的随机变量。如果假设为真，则 x 来自χ²分布，自由度为（s - 1）和（k - 1）。