二维方差分析
- 更新时间2025-07-30
- 阅读时长11分钟
获取两个因子在不同水平上的试验观测数组并进行双因子方差分析。

输入/输出
 A水平数
—
A水平数
—
A水平数是因子a中的水平数。如a为固定效应,A水平数的符号为正;如a为随机效应,a水平的符号设置为负。  X
—
X
—
X包含所有的观测数据。  A水平索引
—
A水平索引
—
A水平索引包含对应观测点的因子A的水平。  B水平索引
—
B水平索引
—
B水平索引包含对应观测点的因子B的水平。  每区间观测点数
—
每区间观测点数
—
每区间观测点数是每个区间内观测点的数量。所有区间的该值相同。  B水平数
—
B水平数
—
B水平数是因子b中的水平数。如b为固定效应,B水平数的符号设置为正;如b为随机效应,b水平数的符号设置为负。  信息
—
信息
—
信息是4×4的矩阵,第一列对应于因子A、因子B、AB交互作用和残差的平方和。第二列是相应的自由度。第三列是相应的均方。第四列是相应的F值。   A显著水平
—
A显著水平
—
A显著水平是因子A的显著水平。  B显著水平
—
B显著水平
—
B显著水平是因子B的显著水平。  AB显著水平
—
AB显著水平
—
AB显著水平是因子A和因子B交互作用的显著性水平。  错误
—
错误
—
错误返回VI的任何错误或警告。将错误连接至错误代码至错误簇转换VI,可将错误代码或警告转换为错误簇。 |
二维方差分析因子、水平和单元
因子是数据分类的依据。例如,以年龄为依据统计个体的仰卧起坐数。对于年龄,可以分为以下水平:
| 水平0 | 6岁至10岁 |
| 水平1 | 11岁至15岁 |
另一个因子为体重,可分为以下水平:
| 水平0 | 小于50公斤 |
| 水平1 | 50公斤至75公斤 |
| 水平2 | 大于75公斤 |
现在,假设已经对仰卧起坐数进行了一系列观测。如对n个人进行随机采样,可能得到如下数据:
| 甲 | 8岁(水平0) | 30公斤(水平0) | 10个仰卧起坐 |
| 第2个人 | 12岁(水平1) | 40公斤(水平0) | 15个仰卧起坐 |
| 第3个人 | 15岁(水平1) | 76公斤(水平2) | 20个仰卧起坐 |
| 第4个人 | 14岁(水平1) | 60公斤(水平1) | 25个仰卧起坐 |
| 第5个人 | 9岁(水平0) | 51公斤(水平1) | 17个仰卧起坐 |
| 己 | 10岁(水平0) | 80公斤(水平2) | 4个仰卧起坐 |
等等。
如观测作为含有两个因子A和B的函数,观测值可表示为以因子A为行、因子B为列的矩阵的单元。每个单元必须包含至少一个观测,每个单元包含观测数量必须相同。
要进行方差分析,您需要指定一个观测值数组 X ,其值分别为 10、15、20、25、17 和 4。数组 Index A 指定了每个观测值所对应的因子 A 的水平(或类别)。在本例中,数组值为0、1、1、1、0和0。
数组B水平索引可指定每个观测的因子B水平或类别。在这种情况下,数组的值为0、0、2、1、1和2。最后,因子 A 有两种可能的水平,因子 B 有三种可能的水平,因此 A 水平 参数的值为 2, B 水平参数的值为 3。
可以采用下列模型中的任意一种,L是指定的每区间观测点数:
- 模型1:固定影响且无相互作用,每个区间(分别对应于因子A和因子B的指定水平x和y)有1个观测点。
- 模型2:固定影响且有相互作用,L > 每区间观1个观测点。
- 模型3:固定影响且有相互作用,L > 1每区间观测点数。
- 模型4:随机影响且有相互作用,L > 每区间观1个观测点。
二维方差分析随机或固定影响
如因子的总体很大且水平不同,要在未对所有水平进行采样的情况下得出结论,因子可视为随机影响。因此,可随机选择水平以期概括所有的水平。如在对所有水平采样后得出结论,因子可视为固定影响。
输入参数A水平数和B水平数分别代表因子A和因子B中的水平数,以及因子为随机或固定影响。例如,如果因子 A 是随机的,则可以将 A 水平 设为负数,即因子 A 的水平数。请注意,如果每个单元格只有一个观测值,则 A 水平 和 B 水平 都必须为正值。即选择模型1。
二维方差分析统计模型
如xpqr是因子A和B在水平p和q的第r个观测点,r = 0, 1, ..., L – 1。
模型1使每个观测点表示为5个部分的和。
xpqr = µ + αp + βq + εpqr模型2、3和4使每个观测点表示为4个部分的和。
xpqr = µ + αp + βq + (αβ)pq + εpqr其中,
βq = µq - µ- µ是总均值响应(总体的均值响应的平均值)。
- αp 是第 p级因子 A 的影响(等于 µp - 其中 µp 是第p 个因子A在所有因子B水平上的平均值)。
- βq 是第 q级因子 B 的影响(等于 µq - 其中 µq 是第q 个因子B在所有因子A水平上的平均值)。
- (αβ)pq 是第 p 个水平的因子 A 和 第q 个水平的因子 B 之间的相互作用(等于 µpq - (µ + αp + βq其中pq 是第 pq个单元的群体平均值)。
- εpqr 是 xpqr 的 偏差。
二维方差分析假设
下列每个假设都以不同的方式表明因子或因子之间的交互对于试验结果没有影响。VI假定影响不存在,然后寻找证据证明假设矛盾。下面有3个假设:
- (A) αp 如果因子A是固定的,则对于所有水平 p ,α p = 0;如果因子A是随机的,则σA² = 0。
- (B) βq 如果因子B是固定的,则对于所有水平 q ,β q = 0;如果因子B是随机的,则σB² = 0。
- (AB) 即 (αβ)pq 如果因子 A 和因子 B 都是固定的,则对于所有水平 p 和 q σA²= 0;如果因子 A 或因子 B 都是随机的,则 σA² = 0。(这不适用于型号1。在模型 1 中不存在交互作用,相关的输出参数是多余的)。
二维方差分析假定
该VI假设:
- 假设对于每个 p、 q和 r,εpqr 为正态分布,均值为 0,方差为σe²。
- 如果一个因子如 A 是固定的,假定在 A 的每一水平上的测量群体都是正态分布,其均值为 α。p +µ,方差σA²,并且每个水平上的所有种群具有相同的方差。此外,假设αp 和为零。对B做相同的假定。
- 如果 A 等因素是随机的,则假设 A 水平本身的影响 αp是均值为 0、方差为σe²的正态分布随机变量。对B做相同的假定。
- 如果与交互作用效果(αβ)相关的所有因素,如A和Bpq 是固定的,假定每个水平上的测量值都是正态分布,均值为 µpq 和方差σAB²。对于任意固定的 p, (αβ)pq 的总和为零。同样,对于任意固定的 q,均值(αβ)pq 的总和为零。
- 如果与相互作用效应(αβ)相关的任何因素,如A和Bpq 是随机的,则假定该效应是一个随机变量 正态分布,其均值为 0,方差为σAB²。如果A是固定的,而B是随机的,那么也假设对于任何固定的 q ,当对所有 p求和时,均值σAB²和为零。同样,如果 B 是固定的,而 A 是随机的,则假设对于任何固定的 p ,当对所有 q求和时,均值σAB²和为零。
- 假定所有作为随机变量的影响都是相互独立的。
二维方差一般方法
在每个模型中,VI使方根的和tss(用于衡量全部总体的总变化)分解为部分方根的和。在模型1中
tss = ssa + ssb + sse因此,在模型2和4中
tss = ssa + ssb + ssab + ssetss中的每个部分和都是对特定因子或因子间的交互作用引起的变化的衡量。ssa用于衡量由因子A引起的变化,ssb用于衡量由因子B引起的变化,ssab用于衡量由因子A和因子B的交互作用引起的变化,sse用于衡量由随机函数引起的变化。注意,在模型1中没有ssab项。说明没有交互作用。
VI使ssa、ssb、ssab和sse分别除以其自由度,得到均方根msa、msb、msab和mse。如因子A对试验观测有强烈的影响,则均方根msa很大。
检验二维方差分析假设
对于每个假设,VI通过计算数字f,得到相关显著水平概率。例如,对于假设(A),即αp =0(固定A),VI计算如下
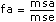
则
sigA = Prob{Fa – 1, (a – 1)(b – 1)} > fa其中
Fa – 1, (a – 1)(b – 1)是自由度为a - 1和(a - 1)(b - 1)的F分布。然后,通过A显著水平、B显著水平和AB显著水平确定何时拒绝相关假设(A)、(B)和(AB)。
何时拒绝虚无假设?对于每个假设,选择一个显著水平。显著水平是错误拒绝某个假设的可能性,通常选择0.05。使所选显著水平与相关的显著水平概率输出进行比较。如显著水平概率小于所选显著水平,则应该拒绝该零假设。
例如,如果A是随机效应,您选择的显著性水平为0.05,而输出 sigA 为0.03,那么您必须拒绝假设αA² = 0,并得出结论:因素A对实验观察结果有影响。
二维方差分析公式
如xpqr是因子A和因子B在水平p和q的第r个观测点,r = 0, 1, ..., L – 1。
如
a = |A水平数|
b = |B水平数|








则



如L > 1,dofab = (a – 1)(b – 1)
如L = 1,dofab = 0

如L > 1,dofe = ab(L – 1)
如L = 1,dofab = (a – 1)(b – 1)





sigA =Prob{Fa - 1, ab(L - 1) > fa} 如果B是固定的
如果B是随机的,则sigA =Prob{Fa - 1, (a - 1)(b - 1 ) > fa}
sigB =Prob{Fa - 1, ab(L - 1) > fb},如果A是固定的
sigB =Prob{Fa - 1, (a - 1)(b - 1 ) > fb},如果A是随机的
AB显著水平 = 概率{F(a – 1)(b – 1), ab(L – 1) > fab}