计算输入序列FFT{X}的反离散傅立叶变换(IDFT)。必须手动选择多态实例。


icon

输入/输出

  • c2dcdb.png FFT {x} —

    FFT {X}是值为复数的输入序列。

  • cbool.png 移位？ —

    移位？指定DC元素是否位于FFT {X}中心。默认值为FALSE。

  • i2dcdb.png X —

    X是FFT{X}的反复数FFT。

  • ii32.png 错误 —

    错误返回VI的任何错误或警告。将错误连接至错误代码至错误簇转换VI，可将错误代码或警告转换为错误簇。

    • 仅当FFT{X}是实数时域信号的傅立叶变换时，才使用该VI的反实数FFT和二维反实数FFT实例。其他情况下，应使用反复数FFT和二维反复数FFT实例。FFT{X}是实数时域信号的傅立叶变换时，FFT {X}是共轭中心对称的，“反实数FFT”和“二维反实数FFT”实例只用于FFT{X}的前部。

    FFT{X}是实数时域信号的傅立叶变换且移位？为FALSE时，FFT {X}的共轭中心对称属性如下图所示。

    1. FFT{X}是长度为N的一维实数时域信号的傅立叶变换时，FFT {X}可由前半部分创建。FFT {X}前半部分和后半部分的中心对称关系可表示为：

      ,

      fi是FFT {X}中元素的个数。

      “反实数FFT”实例只使用前半部分：从f0至f_进行反实数FFT，是向下取整运算。

    2. FFT{X}是M行N列的二维实数时域信号的傅立叶变换时，FFT {X}的下半部分可由上半部分创建。FFT {X}上半部分和下半部分的中心对称关系可表示为：

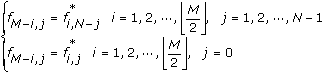
      fi,j是FFT {X}中元素的个数。

      “二维反实数FFT”实例只使用前半部分：从f0.0至f_进行二维反实数FFT，是向下取整运算。

    该函数使用FFT算法计算向量或矩阵FFT {X}的反离散傅立叶变换(IDFT)。移位？输入指定FFT {X}输入端是否为以直流为中心的FFT。

    对于一维，N个采样的频域序列Y，IDFT的定义如下：

    n = 0, 1, 2, …, N–1，

    对于二维，N×N的频域数组Y，IDFT的定义如下：

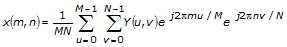
    m = 0, 1, …, M–1，n=0, 1, …, N–1